游戏中的寻路系统

在前面的章节中我们已经讨论了如何在位置变化时做移动同步。对于由客户端操控的entity来说，其位置更新主要是由客户端的输入来驱动的。而对于服务端管理的NPC等类型的entity来说，则是由AI发起的寻路任务驱动的。这个寻路任务主要包括三种：

1. 移动到特定点的指定半径内
2. 趋近特定可移动entity的指定半径内
3. 跟随特定可移动entity，维持与这个entity的距离在一定半径内

跟随移动可以通过不断的调用趋近移动来完成，而趋近移动则可以通过不断的调用指定点的移动来完成，所以寻路任务可以简化为如何一个entity从A点移动到B点，这个任务的核心问题就是从地图上找出两点之间的一条可移动路径。在不同的游戏世界中，不同的entity的可移动区域可能各有规定，例如在同一个3D空间，有些entity只能在地面行走，有些entity有攀爬功能可以在岩壁上移动，甚至有些entity可以在空中飞行水下潜行。针对不同的移动能力，我们需要对游戏场景采用不同的结构来表示可移动区域，并使用不同的寻路算法来计算两点之间的可移动路径。下面我们来针对游戏中常见的地图类型来介绍其可移动区域的结构建模以及路径查询。

基于图的寻路

游戏地图中最简单的用来描述可移动区域的结构就是图。在图论中，一个图G的数学定义为G=(V, E)，其中V为图G中的节点集合，而E为图G中的边集合，每条边都由(v1, v2)这个二元组来表示，v1,v2都属于节点集合V。如果E中不区分二元组内两个元素的顺序，即(v1, v2)等价于(v2, v1)，则这个图称之为无向图，反之称之为有向图。下图中就是上海的地铁线路图的一部分，他也可以转换为一个无向图：

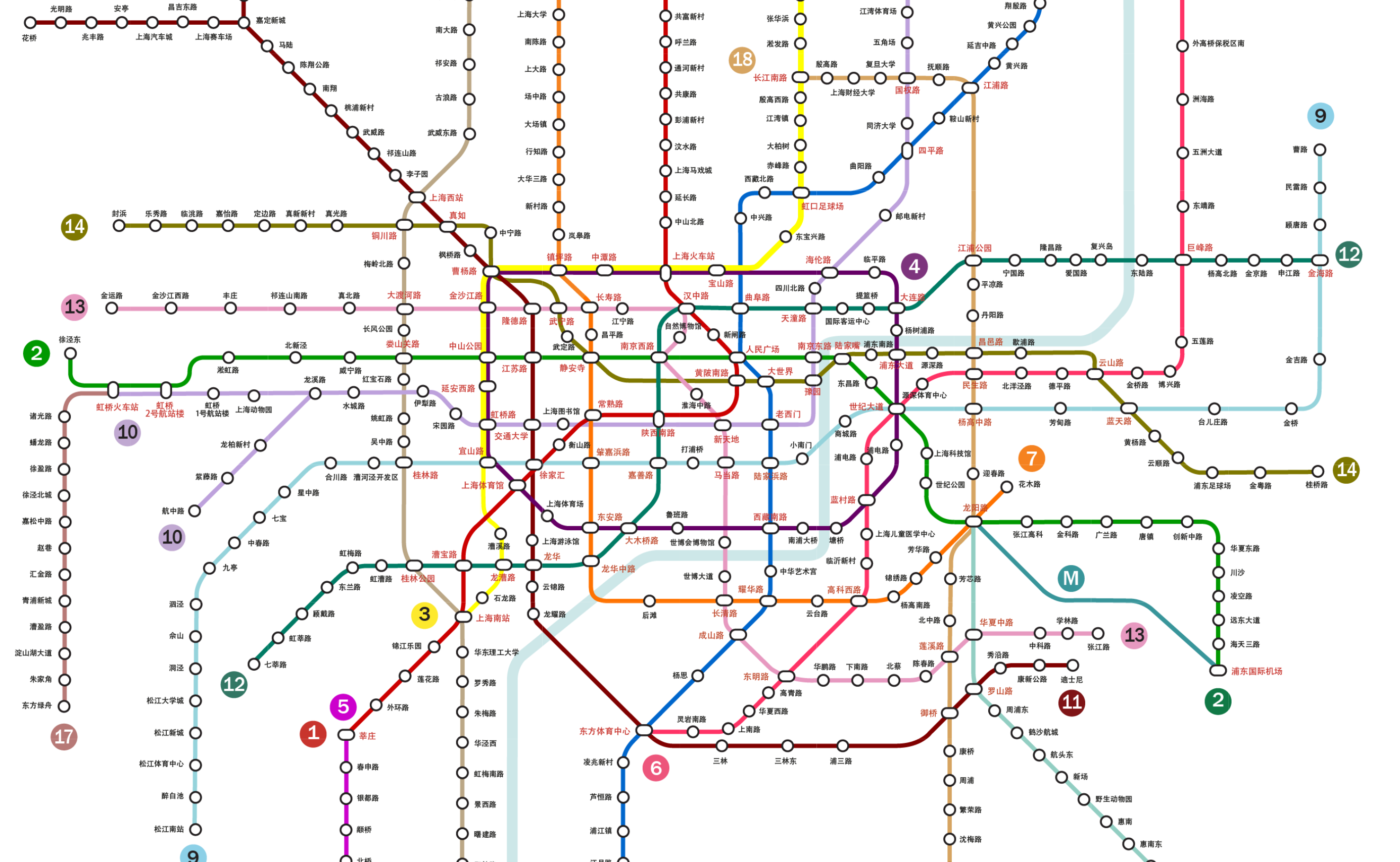
如果存在一个有序节点列表v[0],....,v[n]，将其内部所有元素与后面一个元素相连接构造出来的(v[0], v[1]),..., (v[n-1],v[n])所代表的n条边都在图G的边集合E中，则定义v[0], v[n]两者之间是连通的，(v[0], v[1]),..., (v[n-1],v[n])是这两个节点之间的连通路径。如果图中任意两点都是连通的，那么图被称作连通图。如果此图是有向图，则称为强连通图。由于无向图可以通过将一条边(v1, v2)转换为两条顺序相反的有向边的方法来构造有向图，所以后文中我们只讨论有向图。

我们前面提出的两点之间的可移动路径查询问题现在可以标准化为一个数学问题：在给定的图G=(V, E)中，从集合V中选取两个不同的点a, b，计算出a->b的连通路径。这个问题可以认为是一个已经解决的数学问题，在算法导论中提供了两种算法来解决这个问题，宽度优先搜索和深度优先搜索，分别简称为BFS(breadth-first-search)和DFS(depth-first-search):

1. 宽度优先搜索时，我们构建一个队列Q，一个集合O以及一个映射P，初始时将a压入Q，同时O.add(a)。然后不断的对Q进行pop操作获取元素c，将由c作为开始节点的所有边的终点d放入到Q中。往Q中push任意一个元素d时都需要检查O中是否已经包含d, 如果包含的则不处理这个元素;如果不包含才能执行push，同时此时记录P[d]=c。当遇到d==b时，则认为找到一条路径L，不断的执行e=P[d],L.add((e, d)),d=e这个迭代，直到d==a，此时reverse(L)就是所需要寻找的一条从a到b的连通路径。当Q为空时，则代表a到b的连通路径不存在。

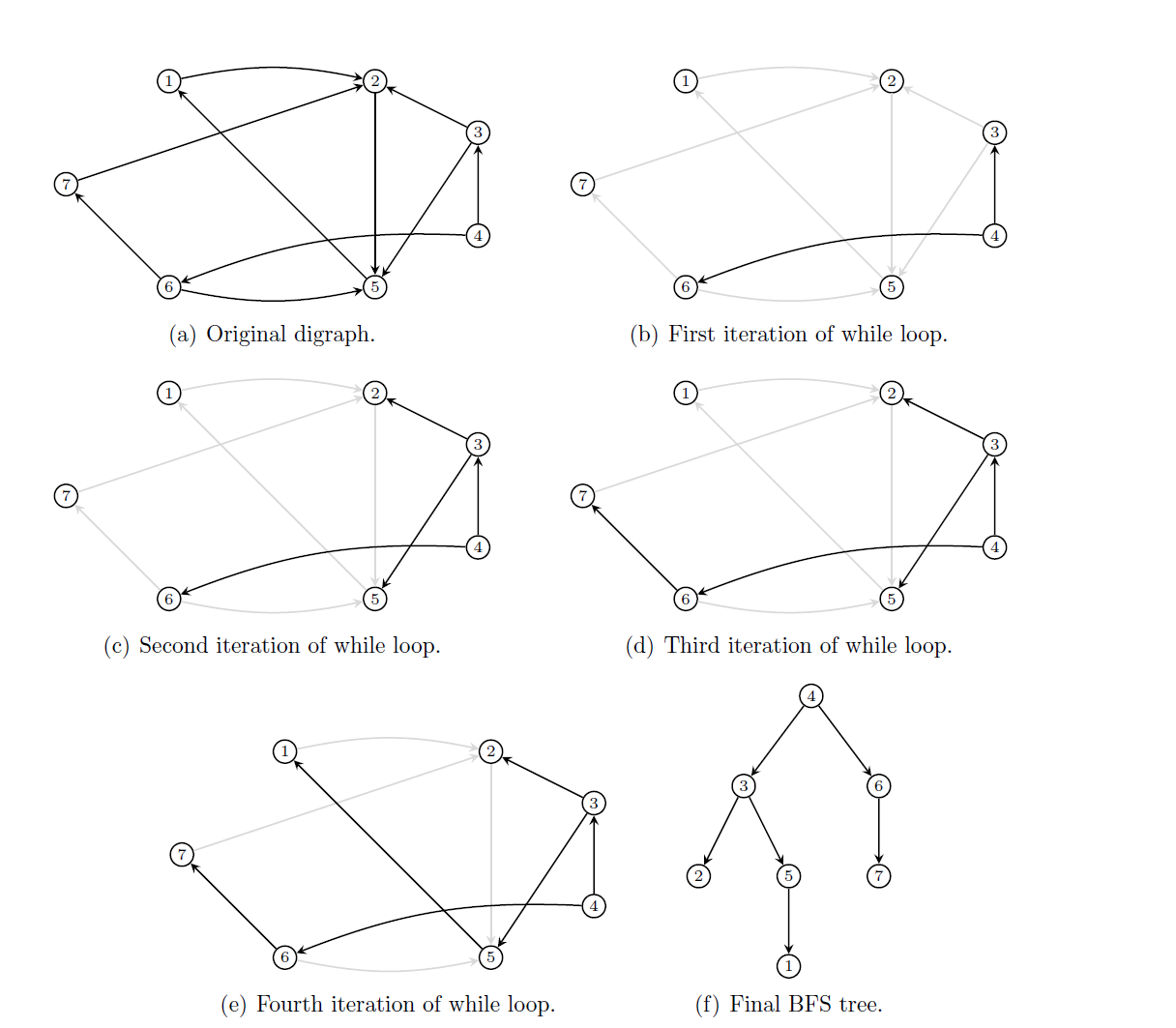
2. 深度优先搜索时，我们类似的构造一个集合O以及一个映射P，同时定义一个函数dfs(c)，这个函数接受一个节点c作为参数，函数体则对由c作为开始节点的所有边的终点d执行if !O.exist(d) then O.add(d),P[d]=c,dfs(d)操作。然后我们调用dfs(a)来触发递归调用，当遇到d==b时，则认为找到一条路径L，不断的执行e=P[d],L.add((e, d)),d=e这个迭代，直到d==a，此时reverse(L)就是所需要寻找的一条从a到b的连通路径。如果dfs(a)完成调用后仍然没有找到一条连通路径，则代表a到b的连通路径不存在。

上面两个路径搜索方法的最坏情况下都需要遍历所有的边，例如图中的所有点构成一个圆环，所以其最坏时间复杂度都是边数量的常数倍。其一般情况下的复杂度也没有优劣之分，不过实际上采用的都是宽度优先搜索，因为深度优先搜索会使用递归，递归带来的性能影响在函数体比较小的时候非常明显，使用栈去模拟递归又要写很多额外代码。

如果a,b两点之间并不连通，则不管是BFS还是DFS都会搜索所有可以由a到达的节点集合S，遍历整个集合S之后才能判定两者无法连通。例如搜索从杭州到三亚的高铁换乘路线会穷尽国内基本所有的高铁站。此时的搜索效率是非常低的，为了最终判定两者不连通会浪费很多时间。所以在游戏实际使用的地图中，一般还会有一个数据结构来辅助查询a,b两点之间是否连通，路径搜索时如果发现这两个点压根就不连通的话就不再执行后续的BFS或DFS过程。直接在离线情况下预处理地图生成unordered_map<int, unordered_set<int>> connected这样的连通性矩阵耗时耗力，而且其存储空间也要求很多，我们需要一个更优秀的结构去处理连通性问题。

对于无向图来说，这个连通查询结构很好做，只需要在每个节点上增加一个字段region_id，所有region_id相同的节点对a,b都是可以连通的，region_id不同的节点对a,b都是不连通的。下面的代码就负责预处理整个地图给所有的节点都赋值相应的region_id：

struct vertex
{
	int id;
	int region_id = 0;
	unordered_set<int> edges;
};

void set_region_id_for_vertexes(unordered_map<int, vertex>& all_vertexes)
{
	int region_id_counter = 0;
	for(auto& [one_id,one_vertex]: all_vertexes)
	{
		if(one_vertex.region_id != 0)
		{
			continue;
		}
		region_id_counter++;
		queue<int> bfs_queue;
		bfs_queue.push(one_id);
		while(!bfs_queue.empty())
		{
			auto temp_id = bfs_queue.front();
			bfs_queue.pop();
			auto& cur_bfs_vertex = all_vertexes[temp_id];
			if(cur_bfs_vertex.region_id != 0)
			{
				continue;
			}
			cur_bfs_vertex.region_id = region_id_counter;
			for(const auto& one_edge: cur_bfs_vertex.edges)
			{
				bfs_queue.push(one_edge);
			}
		}
	}
}

由于每个节点只会设置region_id一次，每条边也只会遍历到一次，所以整体的消耗时间等价于边的数量加上节点的数量，是线性复杂度，非常高效。

而对于有向图来说，情况复杂了起来，只用region_id是不够的，我们不能因为a->b有一条路径就将这两个点的region_id设置为同一个值，因为可能b->a并没有可行路径。有用同一个region_id的集合S内的任意两点a,b都需要能找到a->b的路径和b->a的路径，即S是图G中的一个强连通子图。我们从G中以下面的方法构造一个新的图G2：遍历G中的每个强连通子图S，删除原来两个点都在S内的边，将整个子图S里的点都替换为同一个新的点v2,对应的更新边的集合E进行节点替换以及重复边的去重。这样我们就得到了一个节点数量和边数量都精简很多的新的有向无环图DAG(Directed Acyclic Graph)G2`。 TODO 换图 自己画一个

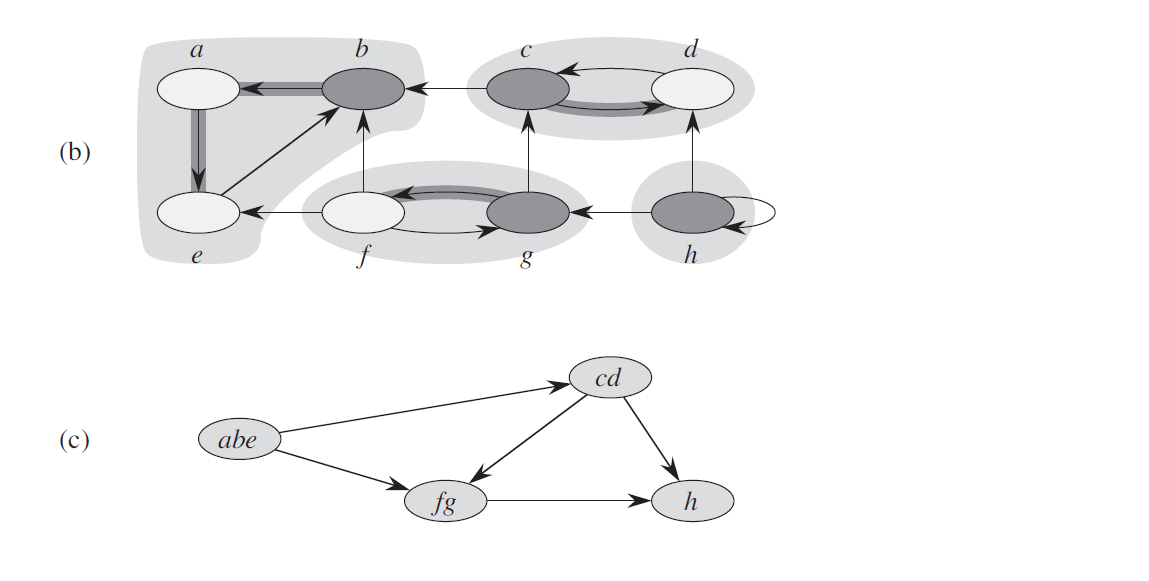
判断原来图G中两个点a,b是否可连通只需要去判断a所在的强连通子图Sa在G2中的点Va与b所在的强连通子图Sb在G2中的点Vb是否连通。由于G2的规模相对G来说小了很多，其连通性判定会节约很多时间，同时对于内存的要求也相对于前述的连通性矩阵降低了很多。现在遗留下来的问题就是我们如何将图G切分为多个强连通分量。

在有向图G中寻找其内部所有强连通分量这个问题已经有现成的算法，叫Tarjan算法。在介绍该算法之前，我们需要先回顾一下前面介绍的DFS, 这里引入一个DFS生成树的结构，来记录DFS时每个节点的前序节点。我们以下面的有向图为例：

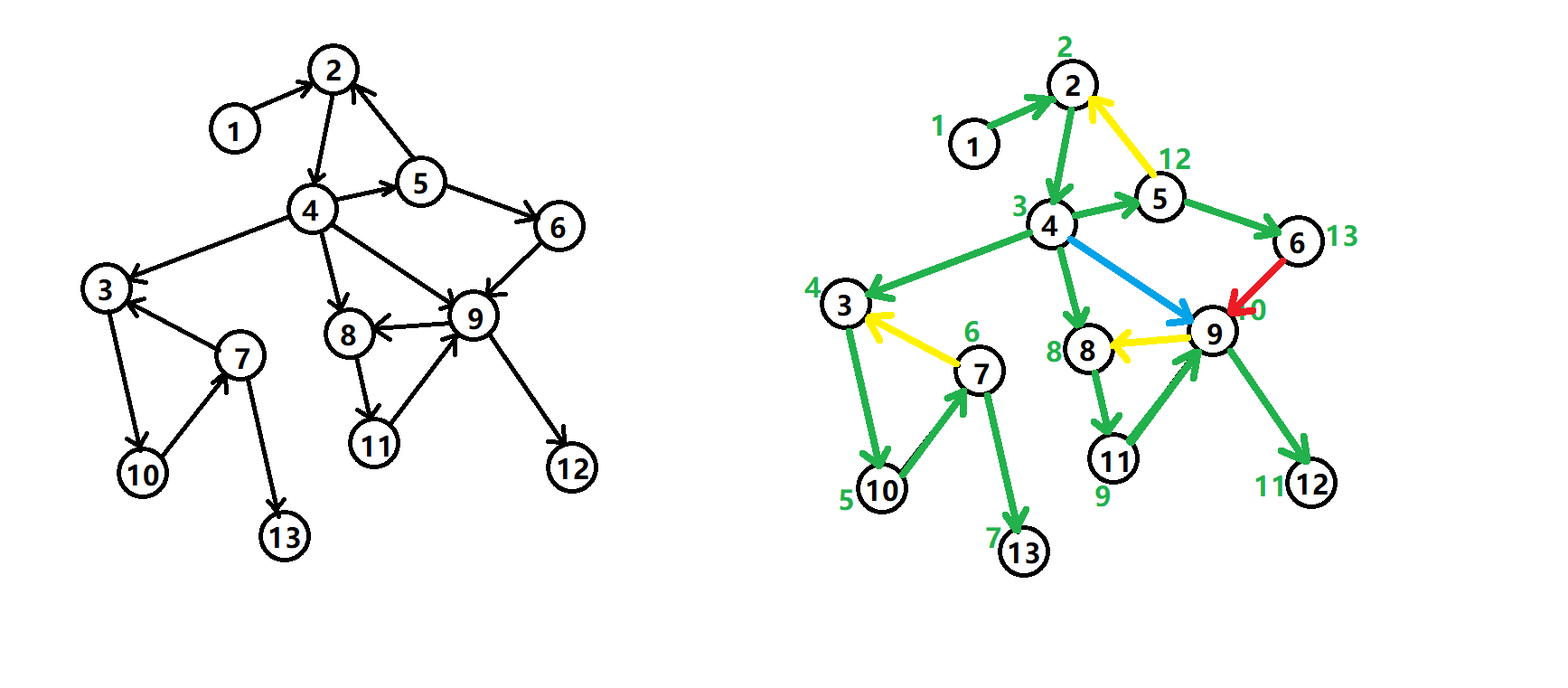
有向图的 DFS生成树主要有4种边（不一定全部出现）：

1. 树边(tree edge)：绿色边，每次搜索找到一个还没有访问过的结点的时候就形成了一条树边。
2. 反祖边(back edge)：黄色边，也被叫做回边，即指向祖先结点的边。
3. 横叉边(cross edge)：红色边，它主要是在搜索的时候遇到了一个已经访问过的结点，但是这个结点并不是当前结点的祖先时形成的。
4. 前向边(forward edge)：蓝色边，它是在搜索的时候遇到子树中的结点的时候形成的。

有了上述定义之后，我们可以利用DFS来计算图的所有强连通分量：如果结点u是某个强连通分量在搜索树中遇到的第一个结点，那么这个强连通分量的其余结点肯定是在搜索树中以u为根的子树中。u被称为这个强连通分量的根。为了证明这个性质我们采取反证法：假设有个结点v在该强连通分量中但是不在以u为根的子树中，那么u到v的路径中肯定有一条离开子树的边。但是这样的边只可能是横叉边或者反祖边，然而这两条边都要求指向的结点已经被访问过了，这就和u是第一个访问的结点矛盾了。

在Tarjan算法中为每个结点u维护了以下几个变量：

1. dfn[u]：深度优先搜索遍历时结点u被搜索的次序。
2. low[u]：设以u为根的子树为Subtree(u)。low[u]定义为以下两类结点的dfn的最小值：
   1. Subtree(u)中的结点；
   2. 从Subtree(u)通过一条不在搜索树上的边能到达的结点。

一个结点的子树内结点的dfn都大于该结点的dfn。从根开始的一条路径上的dfn严格递增，low严格非降。按照深度优先搜索算法搜索的次序对图中所有的结点进行搜索。在搜索过程中，对于结点u和与其相邻的且不是u的父节点的结点v考虑3种情况:

1. v未被访问：继续对v进行深度搜索。在回溯过程中，用low[v]更新 low[u]。因为存在从u到v的直接路径，所以v能够回溯到的已经在栈中的结点，这里就包括u。
2. v被访问过，已经在栈中：即已经被访问过，根据low值的定义（能够回溯到的最早的已经在栈中的结点），则用dfn[v]更新low[u]。
3. v被访问过，已不在在栈中：说明v已搜索完毕，其所在连通分量已被处理，所以不用对其做操作。 下面的就是上述算法的伪代码：

TARJAN_SEARCH(int u)
    vis[u]=true
    low[u]=dfn[u]=++dfncnt 		// 为节点u设定次序编号和Low初值
    push u to the stack 		// 将节点u压入栈中
    for each (u,v) then do 		// 枚举每一条边
        if v hasn't been search then  // 如果节点v未被访问过
            TARJAN_SEARCH(v) 	      // 继续向下搜索
            low[u]=min(low[u],low[v]) // 回溯
        else if v has been in the stack then // 如果节点u还在栈内
            low[u]=min(low[u],dfn[v])
    if (DFN[u] == Low[u]) // 如果节点u是强连通分量的根
　　 repeat v = S.pop  	// 将v退栈，为该强连通分量中一个顶点
　　 print v
　　 until (u== v)

对于一个连通分量图，我们很容易想到，在该连通图中有且仅有一个dfn[u]==low[u]。该结点一定是在深度遍历的过程中，该连通分量中第一个被访问过的结点，因为它的dfn值和low值最小，不会被该连通分量中的其他结点所影响。因此，在回溯的过程中，判定dfn[u]==low[u]的条件是否成立，如果成立，则栈中从u后面的结点构成一个强连通分量。整个算法需要执行两次DFS，所需时间为图G的大小的线性时间。

前述内容解决了如何在有向图中寻找a,b两点的一条连通路径的问题，但是寻路问题并不是简单的获取一条连通路径，因为在连通路径有多条的情况下，我们更希望获取一条消耗最低的路径。

为了定义路径的消耗，我们需要对图G中的每条边增加一个cost，代表路过这条边时需要增加的代价，而一条路径的总cost则是路径中所有边的代价之和。

在给定的无负的cost的有向图G中寻找给定两个节点a,b的最短路径是一个已经解决的问题，使用的是经典的Dijkstra单源最短路径算法。Dijkstra算法负责计算一个点到图内其他点的最短距离，主要内容是维护两个集合，即已确定最短路径的结点集合CloseSet(A)、这些结点向外扩散的邻居结点集合OpenSet(B)，同时还维护两个数组:

1. 一个距离数组dis来记录每个节点到起点a的距离，初始时都是负无穷大，同时dis(a)初始化为0。
2. 一个前序数组pre来记录每个节点到起点a的最短路径中的最后一条边的起点。

在初始化上述变量之后，程序逻辑如下：

1. 把起点a放到A中，把每条以a为起点的边的终点v放到B中，更新dis(v) = cost(a,v)。
2. 从B中找出dis(u)最小的节点u，放到A中。
3. 把每条以u为起点的边的终点v进行如下处理：
   1. 如果v已经在集合A中则不做处理，
   2. 如果v不在集合A中，则加入到集合B，同时计算temp_cost= dis(u)+cost(u,v)。如果这个temp_cost小于已经记录的dis(v)则更新dis(v)=temp_cost同时更新pre[v]=u。
4. 重复步骤2和步骤3，直到B为空

上面的算法流程就是dijkstra算法的完成流程，朴素的dijkstra实现在步骤2中直接遍历所有元素来获取最小值，此时算法的时间复杂度为|V|*|V|, 采取了斐波那契堆优化之后，最优复杂度可以降低到|E| + |V|log(|V|)。

由于我们目前只需要计算a,b两点之间的最短路径，所以在步骤2中发现u==b时就可以提前结束算法迭代。算法结束时如果B为空代表a,b不连通，如果u==b代表a,b连通，此时构造结果路径列表L，执行do L.push(u), u=pre[u] while u!=a，执行结束之后reverse(L)就是我们所需要的一条a->b的最短路径。最坏情况下b点恰好是离a最远的一个点，此时计算a,b之间的最短路径需要跑完完整的dijkstra算法，因此计算在图G中计算a,b两点之间的最短路径算法的时间复杂度与dijkstra是一样的。

基于网格的二维平面寻路

如果游戏场景只有x,y两个坐标轴的话，这个场景就是一个二维平面。针对二维平面最简单的可行走区域表示结构为二维网格grid，内部存储了网格内每个基本单元cell存储一个bool值，代表该cell是否可以通行：

struct grid
{
	vector<vector<bool>> cells;
}

将整个二维平面转换为网格的方法也很简单，选取一定粒度的正方形作为cell的形状，然后以这个cell作为单位粒度对原始的场景坐标轴进行变换。如果变换后由(x,y)->(x+1,y)->(x+1,y+1)->(x,y+1)这四个点组成的正方形内有不可同行的区域，则cells[x][y]设置为false，反之设置为true。从x,y出发可以直接移动到达的其他节点根据不同的设定有不同的定义：

1. 只允许往上下左右四个方向移动，即以x,y作为起点的边最多四条，其终点集合为(x+1,y),(x-1,y),(x,y-1),(x,y+1)这四个cell
2. 允许往上下左右左上左下右上右下八个方向移动，即以x,y作为起点的边最多八条，其终点集合为(x+1,y+1),(x+1,y),(x+1,y-1),(x,y-1),(x,y+1),(x-1,y+1),(x-1,y),(x-1,y-1)这八个cell

整个网格地图可以很方便的转换为前述的无向图结构G=(V, E),这里的所有的cells[x][y]==true的x,y坐标构成了当前场景的无向图G中的V节点集合,然后每个(x,y)直接相邻的每个点(m,n)对应的cells[m][n]==true，则将(x,y)->(m,n)加入到边集合E中。假如当前grid中所有cell[x][y]都是true，则此时边集合E内会包含(x*y)*(x*y - 1)/2条边，与grid内的cell数量的二次方成正比，而这些边在grid结构体中不需要额外的字段去存储。所以在二维平面上地图表示主要使用grid，而不是通用的无向图结构。

由于在写代码时四方向移动比八方向移动简单点，所以后面我们主要讨论网格地图上的四方向移动。在grid地图上执行寻路时，我们可以沿用之前使用的dijkstra算法来计算两个cell之间的最短路径：

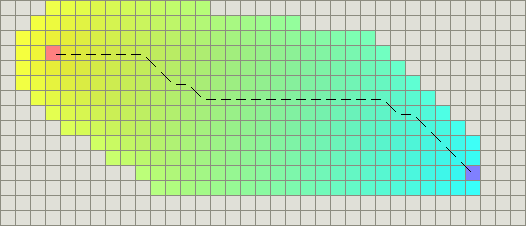
上图就是dijkstra算法在一个grid地图上执行后的结果，粉色方块为起点，紫色方块为终点，白色间隔线段为计算的最短路径，其他的彩色格子代表算法执行过程中遍历到的其他节点。可以看出在这个全连通grid上dijkstra算法计算出一条长度为n的最短路径时，所遍历到的cell数量为n*n，这种时间复杂度对于稍微长一点的路径来说不可接受，但这却是计算最短路径不可避免的代价。如果我们放松对路径长度的最短需求，只要求寻路时获取一条局部最优的连通路径，将极大的减少节点的搜索空间，降低搜索的整体运行时间。在这个思想的指导下，基于dijkstra算法的A*路径搜索算法被提出。dijkstra算法维护了一个代表距离起点具体的dis数组，而在A*算法中维护了三个数组:

1. g数组，g[n]代表从起点a到节点n的最短距离，等价于dijkstra中定义的dis数组,称之为实际cost
2. h数组，h[n]代表n点到终点b的预估距离，也叫启发cost,这个预估距离的函数可以任意自定义
3. f数组，f[n]=g[n]+h[n],代表经过n点的从a到b的局部最优路径的估算距离,

在给出上述变量的定义之后，我们再来描述A*路径搜索的算法流程：

1. 把起点a放到A中，把每条以a为起点的边的终点v放到B中，更新g[v] = cost(a,v)，同时计算h[v]以及f[v]。
2. 从B中找出f[u]最小的节点u，
   1. 如果u==b则构造结果路径列表L，执行do L.push(u), u=pre[u] while u!=a，执行结束之后reverse(L)就是我们所需要的一条a->b的最短路径
   2. 如果u!=b,则将u放到A中。
3. 把每条以u为起点的边的终点v进行如下处理：
   1. 如果v已经在集合A中则不做处理，
   2. 如果v不在集合A中，则加入到集合B, 计算temp_cost= g[u]+cost[u,v]，如果h[v]没有计算过则计算h[v]。如果这个temp_cost小于已经记录的g[v]则更新g[v]=temp_cost同时更新pre[v]=u, f[v]=g[v]+h[v]。
4. 重复步骤2和步骤3，直到B为空

如果算法结束时仍然无法从步骤2中返回结果路径，则代表a,b两点之间无连通路径。下图中就是将h[n]设置为n->b的最短距离时的A*执行结果：

A*算法的执行速度和路径质量严重依赖于h[n]函数的选择：

1. 如果h[n]等价于n到b的最短路径的cost，则搜索时只会遍历到a,b最短路径上的节点，此时执行速度最快，同时返回的也是最短路径
2. 如果h[n]小于n到b的最短路径的cost，则搜索时会遍历到更多的节点，但是返回的依旧是最短路径。h[n]越小则遍历的节点越多，算法执行的越慢。如果我们将启发函数h[n]设置为返回常量0之后，上述流程就等价于dijkstra的算法流程,返回的是最短路径
3. 如果h[n]大于n到b的最短路径的cost，则算法终止时返回的路径不保证是一条最短路径，但是此时遍历到的节点数量相对于dijkstra来说会少。这个h[n]与真实距离之间的差异越大，遍历的节点空间数量越少。当h[n]相对于g[n]有数量级的差异时，退化为纯的贪心搜索，即步骤2每次获取离目标点预估距离最小的点。

如果我们无法指定一个简单高效的函数来获取n到b的最短路径的cost，所以我们只能希望将h[n]设置的足够大来加速算法的执行，但是太大又会退化成贪心算法影响路径的质量（完全不考虑最短路径的计算结果）。所以实际使用中一般将h[n]设置为在无障碍物的情况下n->b的最短路径距离乘以一个（1,10]区间内的系数。在无障碍物的情况下，在四方向移动时的两点之间的最短距离为曼哈顿距离(Mahattan Distance)，其计算方式为计算两点的坐标插值的两个分量的绝对值之和，计算时间为常数，在八方向移动时也有一个类似的切比雪夫距离(Chebyshev distance)，其计算时间也是常数。另外还有一个常规的距离计算函数欧几里得距离(Euclidean distance)，这个就是平面中两点的直线距离，如果选用这个函数作为启发距离计算，则要小心的挑选其常数系数，以保证最后的结果要大于最短路径距离。下图就是在支持八方向移动的地图中使用常数为1的欧几里得距离时的A*算法执行结果，可以看出获取了一条最短路径，同时节点搜索空间还是有很多冗余：

A*算法是所有带空间位置信息的寻路搜索算法中应用最广的算法，通过添加到目标点的启发距离cost，算法迭代时以贪心的方式选择下一个需要考虑的节点，可以极大的减小CloseSet(A)、OpenSet(B)的大小，从而加速整体的路径搜索流程。不过在可以八方向移动的二维网格上，有一个更优的JPS(Jump Pointer Search)算法，这个算法是由Daniel Harabor和Alban Grastien在2011年的论文Online Graph Pruning for Pathfinding on Grid Maps中提出的。在2012到2014年举办的三届基于Grid网格寻路的比赛GPPC（The Grid-Based Path Planning Competition）中，JPS已经被证明是基于无权重格子，在没有预处理的情况下寻路最快的算法。这种近乎于标准答案的JPS算法最终导致了GPPC的停办。

JPS算法也是基于A*算法的思想改造而来，其主要差异在于选取了一个点进入CloseSet之后应该将哪些点引入OpenSet中。在A*算法中，会将这个点的周围八个邻居节点中的所有非障碍物节点都尝试加入到OpenSet中，而JPS算法则会排除掉很多不必要的邻居节点。下面我们来分析JPS的邻居节点排除过程，这里我们规定沿着坐标轴移动到邻居的cost为1，而沿着对角线移动到邻居的cost为sqrt(2)。

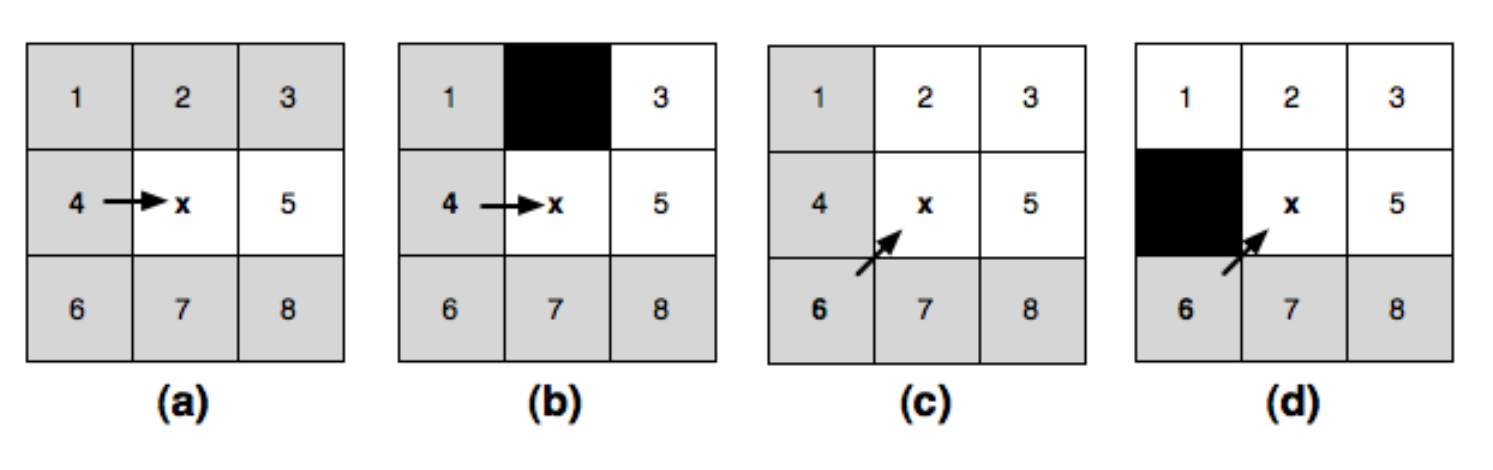
我们先来考虑沿着坐标轴移动的情况，由于四个坐标轴的分析是对称的，所以我们只讨论向右移动的情况，见上图中的a。此时我们获取了一个新的CloseSet节点x，其父节点是网格4，我们来决定接下来将如何筛选x的八个邻居进入到OpenSet。对于这八个节点中的某个节点n，如果总是可以将4->x->n替换为一条更优的路径4->m或者4->x->m，则我们可以把这个点n安全的筛除，不再考虑进入OpenSet:

1. 首先可以排除的是节点4，因为4->x->4是一个回路，在路径上删除此回路会获得一条更短的路径，
2. 然后可以排除1,2,6,7这四个点，因为4可以直接连接这四个点，直连距离都比经过x后的距离短，
3. 最后排除3,8两个点，因为4->x->3的长度等于4->2->3的长度，4->x->8的长度等于4->7->8的长度。所以某条路径中如果包含了4->2->3，总是可以安全的替换为4->x->3，此时出现了等价最短路径的情况。从4移动到节点3出于贪心的考虑我们会选择离3最近的节点2而不是节点x。因此我们将节点3排除，同样的理由我们排除了节点8。

所以在无障碍物的情况下，由4->x之后，我们只需要考虑将节点5加入到OpenSet中。接下来我们考虑存在障碍物的情况：

1. 如果节点1或者节点6是障碍物，不影响之前的判断，因为路径更优的要求下，我们在任何情况下都不会移动到1或者6
2. 如果节点2或者节点7是障碍物，由于上下对称我们只讨论2是障碍物的情况，即上图c，此时4->2->3不再连通，4->x->3成为了4->3之间的唯一一条最短路径，因此我们无法将3从下一跳节点中排除，需要加入OpenSet。同样的理由如果7是障碍物，我们需要将8加入到OpenSet。这种原来不考虑进入OpenSet的点,在出现了障碍物之后需要进入OpenSet，定义为强制邻点(Forced Neighbours),此时的x被定义为跳点(Jump Point)。
3. 如果节点3或者节点8是障碍物，也不影响之前的判断，因为3和8不会出现在基于目标距离优先的经过4->x的搜索路径中
4. 如果节点5是障碍物，则5不再加入到OpenSet中，

基于类似的分析方式，在上图c描述的在无障碍物的情况下的对角线移动6->x中，我们需要将2,3,5加入到OpenSet；在4为障碍物时，需要加入节点1；在7为障碍物时需要加入节点8。

所以JPS算法就是基于跳点的搜索，不过这里的跳点不仅仅包括前述的由于强制邻居引发的跳点，还包括另外的两种跳点：

1. 路径的起点和终点被定义为跳点
2. 当a->b是一个对角线移动时，由b可以只按照坐标轴移动可以连接到某个跳点，则b也是跳点

给定了跳点的完整定义之后，我们定义一个函数jps_search(m,n)代表从m移动到n之后如何在n点进行继续的搜索：

1. 如果n是终点，则返回
2. 对n进行坐标轴四方向直线搜索, 每个方向直线搜索的停止条件如下：
   1. 遇到障碍物
   2. 超过地图边界
   3. 遇到已经在OpenSet或者CloseSet中的点
   4. 遇到一个跳点k，此时将此跳点k加入到OpenSet，并记录k的父节点为pre[k]=n 停止搜索前遇到的点都加入到CloseSet中。
3. 如果上面的坐标轴四方向搜索没有遇到终点，则分别对四个对角线方向的直接邻居k记录其父节点为pre[k]=n，并递归执行jps_search(n,k) 有了这个jps_search的定义之后，通过JPS算法获取(a,b)之间路径的A*流程如下：
4. 将a加入到OpenSet(B),记录pre[a]=a
5. 从B中获取综合cost最小的节点n，加入到CloseSet(A)
   1. 如果n是终点，则利用pre数组计算完整路径
   2. 如果n不是终点，则调用jsp_search(pre[n], n)进行邻居搜索
6. 不断的执行步骤2,直到OpenSet为空

下面我们以一个实际例子来描述JPS搜索的执行过程，初始设置见下图,绿色为起点，红色为终点，黑色为障碍物：

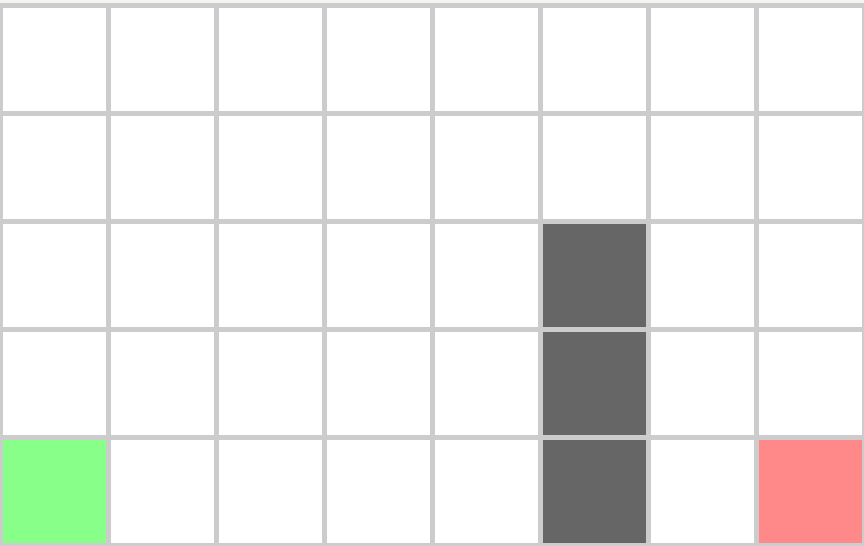
开始时以这个绿色节点执行jps_search，由于坐标轴方向都是障碍物或者地图边界，多次递归之后执行到途中的黄色节点：

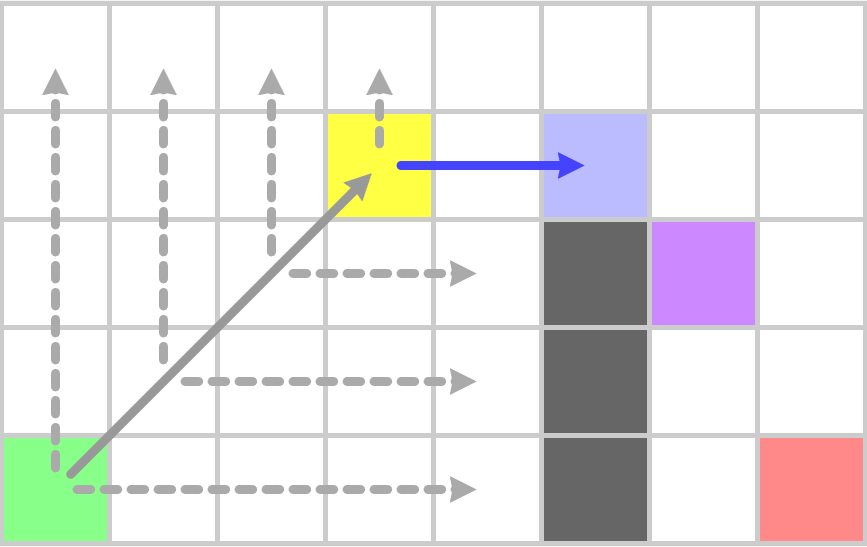
这里之所以会停留在黄色节点是因为浅紫色节点有一个强制邻居即图中的紫色节点，所以浅紫色节点为跳点，而黄色节点可以水平移动到浅紫色节点，根据跳点的定义黄色节点也是跳点，所以本次jsp_search会以黄色节点加入到OpenSet结束。开始下一轮迭代后，从OpenSet中获取了这个黄色节点，并执行jps_search，

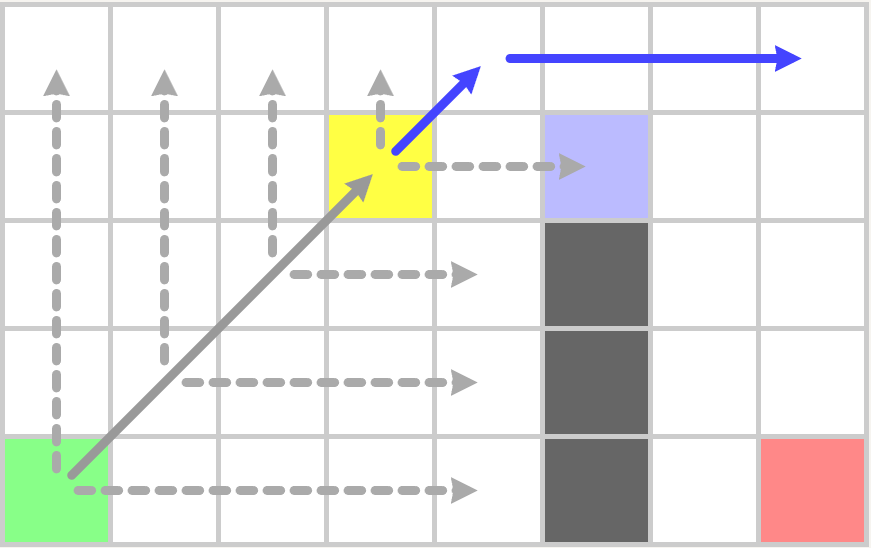
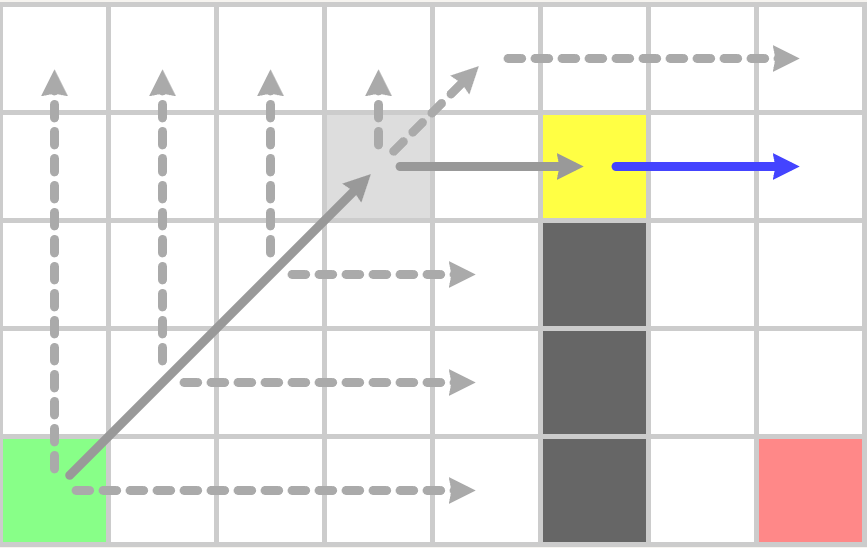
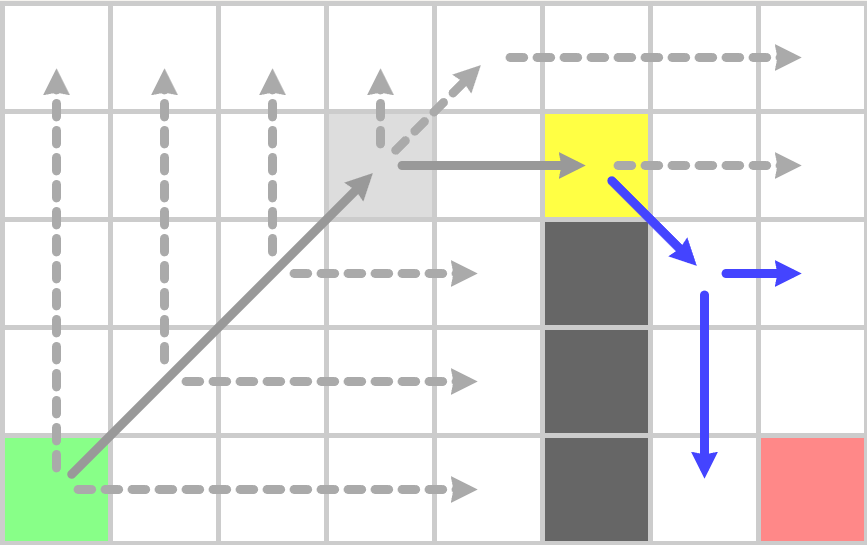
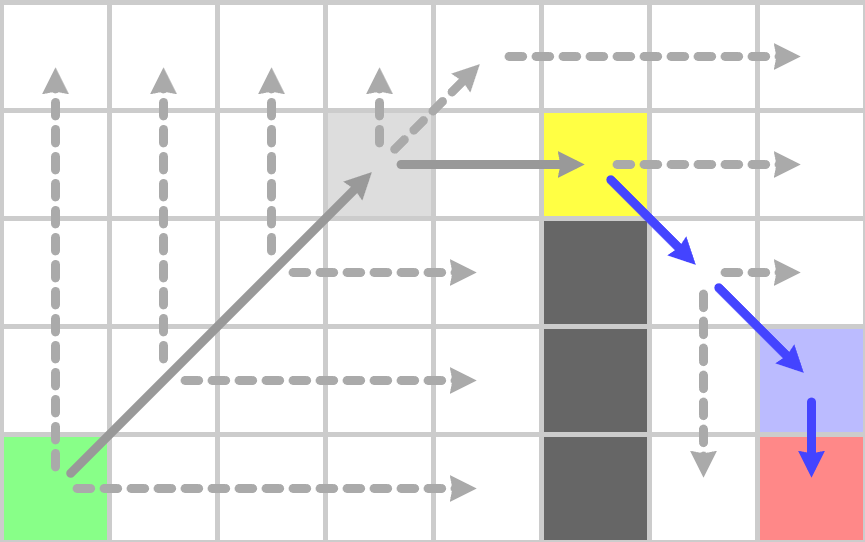
到上图之后遇到了作为终点的跳点，因此终点之前的点也为跳点，加入到OpenSet，再执行一次jps_search之后，OpenSet中只剩目标点，此时构造最终的路径：

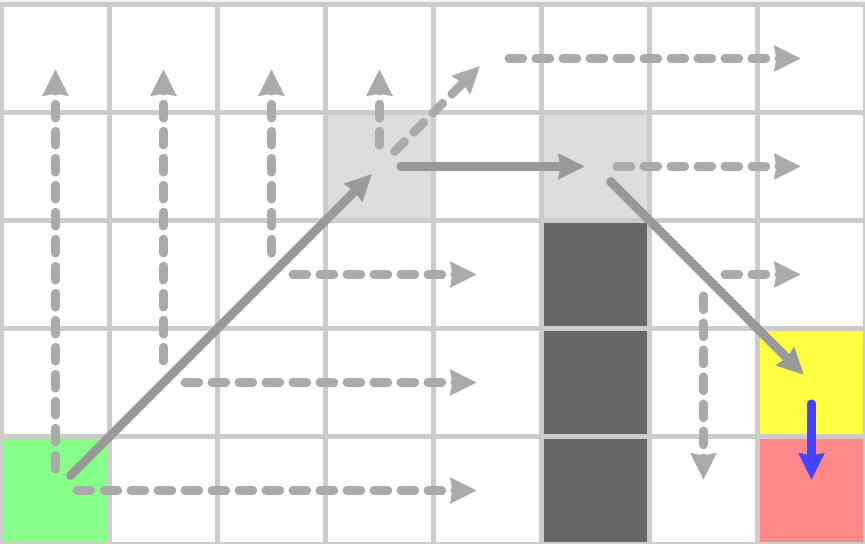
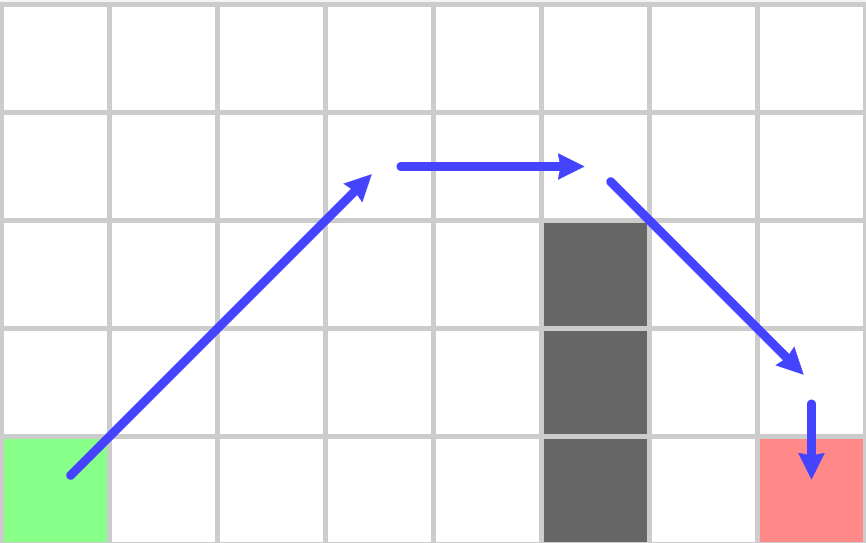
JPS算法相对与A*搜索的优越性在于其OpenSet减少了很多，因此每次迭代时从OpenSet里获取最小值代价很低。不过其CloseSet相对于A*来说增大了很多，因为其四方向坐标轴搜索很有可能探寻到地图边界，所以真正的实现中一般使用bit数组来表示CloseSet，相对于使用std::unordered_set这样可以显著的降低维护CloseSet的内存和CPU时间。

基于体素的三维空间寻路

前面章节讨论的是在二维平面上的网格寻路，然而新千年以来的新游戏基本都是在三维空间内。在三维空间内的寻路可以继续沿用我们在二维空间内网格寻路的相关经验，采用A*算法来搜索连通路径。不过此时的寻路基本单元不再是平面空间内代表长方形的的cell，而是三维空间内代表长方体的的体素voxel，原来存储节点障碍物信息的二维数组也要拓展为三维数组，寻路时查找一个节点的邻居从二维连通变成了三维联通。如果允许体素的对角线连通的话，一个体素可能的邻居节点会有26个，这大大的增加了搜索空间的膨胀速度，所以一般来说体素寻路时只允许体素进行坐标轴方向的移动，一个体素可能的邻居节点数量降低为了6个，此时A*搜索时的启发函数可以使用三维空间的曼哈顿距离，后续的讨论中我们将使用此设定。

不过实际上并不会采取三维数组的形式来存储这些信息，因为其内存占用太大了。对于一个1km*1km*1km的空间，如果采用0.25m*0.25m*0.25m的立方体作为体素的大小，且每个体素占用一个字节，则整体体素的数量为4000*4000*4000字节，约为60GB，即使按照bit来存储也会消耗7GB，这种内存占用是无法接受的。考虑到一般情况下三维场景中障碍物的体积占比很小，绝大部分的体素都是不带有阻挡的，我们可以不存储非阻挡的部分来降低存储整体体素数据的内存占用。同时阻挡区和非阻挡区域很多时候都是由几何体构成的，在一定空间内是连续的。主流的利用这种阻挡体素的稀疏性和连续性的存储结构主要有两种：一种是高度场(height field)，另外一种是八叉树(voxel tree)。

使用高度场存储体素

在定义高度场的存储结构之前，我们先定义一个叫span的概念，这个概念对应垂直坐标轴里一段连续的障碍物体素或者空体素:

struct span
{
	int32 height:16; // 当前span的底部高度
	int32 length:15; // 当前span的连续长度
	int32 is_blocked:1; // 当前span是否是障碍物
};

原有的多个体素所要求的内存空间被一个只占用4个字节的span所代替，因此在内存上节省了很多。在三维空间的xz平面中我们构造一个二维的grid，grid里每个cell都包含对应平面坐标从最低点到最高点的所有span，同一个cell里的所有span按照其height增大的顺序进行排列，相邻的两个span的空间是连续的，即下面的span的height +length + 1等于上面span的height:

struct cell
{
	// 最后一个span的高度为场景最大高度 is_blocked 设置为true 同时length 为1
	span* span_vec;
	int32 span_num;
};
struct height_field
{
	std::vector<std::vector<cell>> xz_cells;
};

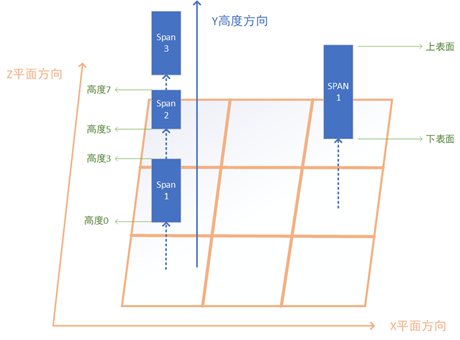
对于一个1000*1000*1000的空体素场景来说，每个cell只需要存储一个span，此时的高度场的总内存大小为1000*1000*(12 + 4)=16MB。

使用span对体素数据存储之后，内存占用减少了，但是对于寻路搜索时却增加了难度，此结构在搜索路径时引入一个重要的问题：如果找到包含(x,y,z)对应的体素的span。此时我们可以利用cell中所有span都按照height增加的方向进行排列的特性，使用二分查找即可找到对应的span。

span* cell::find_voxel(int32 y)
{
	// 这里我们保证最后一个span的高度就是场景的最大高度 同时长度为0
	// 所以temp_iter指向的内存区域永远有效
	auto temp_iter = std::lower_bound(span_vec, span_vec + span_num, y, (const span* temp_span, int32 temp_value)
	{
		return temp_span->height < temp_value;
	});
	if(temp_iter->height == y)
	{
		return temp_iter;
	}
	if(temp_iter == span_vec)
	{
		return nullptr;
	}
	temp_iter--;
	return temp_iter;
}

由于span内包含多个体素，为了记录路径搜索时路过的体素点，我们定义一个新的结构：

struct voxel_node
{
	int32 x,y,z; // 体素对应的坐标
	const span* voxel_span; //体素所在的span
};

接下来我们继续考虑搜索时如果遇到了一个voxel_node，如何获取其可连通的其他voxel_node：

1. 对于竖直方向，直接获取当前span里当前体素对应的的上下两个邻居体素的voxel_node加入到OpenSet，如果某个方向到达了边界，则不添加此方向的邻居体素

2. 对于其他方向，计算对应的(x,y,z)，找到对应的cell，然后使用find_voxel来找到对应的span，如果此span不是阻挡体，则构造voxel_node(x,y,z,span)加入到OpenSet

采用这种方式来计算邻居并加入OpenSet会导致OpenSet变得很冗余，在一个完全连通的n*n*n的立方体区域执行两个对角的寻路会将立方体内的所有体素加入到OpenSet中，空间复杂度为距离的三次方，实际使用时这种复杂度完全无法接受。因此我们需要使用前述的JPS寻路的思想，利用span的连续性，去除冗余节点。假设当前点m在span_a中，通过span_a的另外一个点n直接连通到了xz平面相邻的某个span_b的点o，构造成了一条m->n->o的路径。此时找到m到span_b上距离最短的点i，此时我们可以证明m->i->o的路径长度一定不比m->n->o长。由于两条路径在xz平面上移动的距离一样都是1，所以我们只需要讨论这两条路径在y轴上的不同：

1. 如果m的y大于等于span_b的最大高度，则i点为span_b上高度最高的点，(m,o)之间的高度差等于(m,i)之间的高度差加上(i,o)的高度差，即m->i->o是一条从m到o的最短路径

2. 如果m的y小于span_b的最小高度，则i点为span_b上高度最低的点，(m,o)之间的高度差等于(m,i)之间的高度差加上(i,o)的高度差，即m->i->o是一条从m到o的最短路径

3. 如果m的y在span_b的高度区间内，则i点的高度等于m的高度，(m,o)之间的高度差等于(i,o)的高度差，即m->i->o是一条从m到o的最短路径

TODO 这里加入三张图来做图例

在这三种情况下我们得到了m->i->o的路径长度一定不比m->n->o长的结论，所以所有由m出发到span_b的路径中都只需要考虑i点即可，i点类似与JPS搜索中的跳点概念。所以当我们从OpenSet中选取到一个voxel_node后，获取与这个voxel_node->voxel_span直接连通的所有span,计算当前voxel_node到这些span的最近点，加入到OpenSet中。这里需要在cell上来添加一个辅助函数，来查询与[a,b)区间有交集的所有非空span:

vector<const span*> cell::find_spans(int32 a, int32 b) const
{
	auto temp_span = std::lower_bound(span_vec, span_vec + span_num, a, (const span* temp_span, int32 temp_value)
	{
		return temp_span->height < temp_value;
	});
	if(temp_span != span_vec)
	{
		temp_span--;
	}
	vector<const span*> result;
	while(temp_span->height < b)
	{
		if(temp_span->height + temp_span->length > a)
		{
			result.push_back(temp_span);
		}
		temp_span++;
	}
	return result;
}

对于一个span来说，其离m的最近点只有一个，所以OpenSet中元素的标识可以使用span来代替，而不是用(x,y,z)。此时基于体素的寻路搜索就变成了基于span的寻路搜索，如果目标点在当前span内，则不再执行搜索，直接将目标节点的父节点设置为当前节点，然后使用父节点信息计算起点到终点的连通路径。原来的空心立方体的对角搜索最坏情况降低到了n*n个span，如果采取对角线优先的启发距离，则可以进一步降低到2*n。

使用八叉树存储体素

前述的使用高度场来存储体素数据已经起到了很好的内存削减和寻路搜索加速的效果，不过这个高度场信息只利用了体素数据在y轴上的连续性，在xz这两个轴上的连续性没有被使用。这样就导致了在一个1000*1000*1000的空体素场景中，高度场的总内存大小为1000*1000*(12 + 4)=16MB。为了进一步利用三个轴的体素连续性，研究人员提出了八叉树(Octree)这种结构：

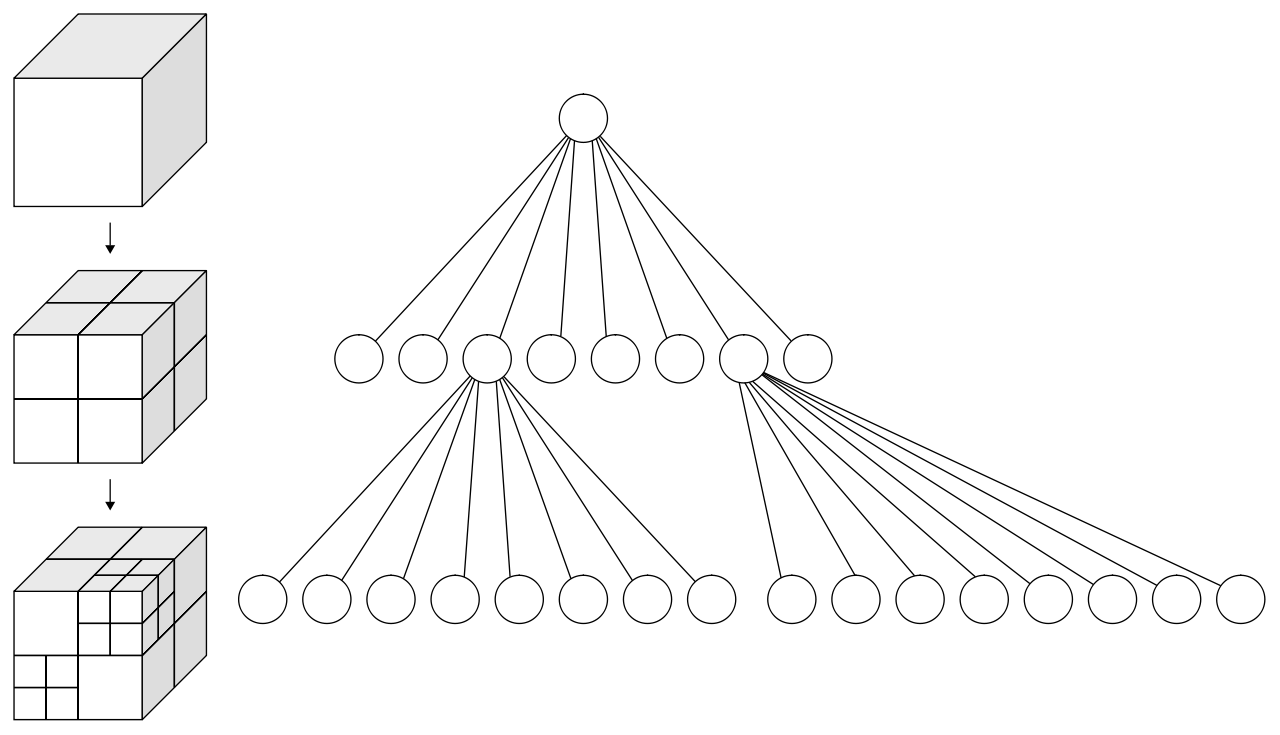
八叉树是一种树形结构，每个非叶子节点都会有八个子节点，每个节点都对应场景中的一个立方体区域，子节点的立方体边长是父节点立方体边长的一半。场景体素的八叉树存储结构采用自顶而下的方法来构建：

1. 获取场景的最小立方体包围盒，构造顶层节点，并加入到未处理节点的队列之中

2. 每次从队列中获取一个节点，判断这个节点对应的立方体区域是否全为阻挡或者全连通，

   1. 如果为全阻挡或者全连通，此时不需要继续划分子节点，只需要在当前节点设置上阻挡标记或者连通标记

   2. 不是全阻挡也不是全连通，需要划分为八个子节点，并将这八个新子节点加入到节点处理队列中

虽然这个八叉树是一个树形结构，不过实际的内存中使用的是基于数组的存储：

struct octree_node
{
	uint32 x:21;
	uint32 y:21;
	uint32 z:21;
	uint32 first_child; // 在下一个layer中他子节点的开始位置索引
	uint32 parent:31; // 父节点在上一个layer中的索引 对于顶层节点来说这个值无意义
	uint8 is_full_block: 1; //是否是全连通或者全阻挡 只有first_child无效时才有意义
};

struct octree_layer
{
	uint32 layer_index;
	float voxel_length;
	std::vector<octree_node> nodes;
};
struct octree
{
	std::vector<octree_layer> layers;
};

最顶层的octree_node为octree.layers.back().nodes[0]。如果octree_node有子节点，则其八个子节点按照特定的顺序在下一层octree_layer::nodes中连续排列，而octree_node->first_child则是第一个子节点在对应下一层octree_layer::nodes中的索引。如果octree_node没有子节点，则first_child设置为numeric_limit<uint32>::max()。octree_node中的(x,y,z)代表以顶层立方体包围盒最低坐标为原点，以当前octree_layer::voxel_length为体素边长计算出来的当前octree_node的体素坐标，这里为了节省空间三个坐标合并为了一个uint64，这也限制了最大层级为21。在最细粒度的体素边长为25cm时，21层所覆盖的最大边长为256km，短期内应该不会有游戏场景的大小超过此长度。

使用这样的结构来存储体素数据可以节省更多的内存占用，对于一个空场景而言只需要存储一个顶层的octree_node即可，也就几十个字节，相对于使用高度场数据的20MB来说是一个非常了不起的优化。如果一个1024*1024*1024的场景里底面最细那一层全是阻挡体，则引入的所有新节点带来的内存占用为1024*1024*2*16*8/7=36MB，而高度场需要加入的新span所需内存为1024*1024*4=4MB，加上之前空场景所需的16MB也比八叉树占用的数据小。为了继续维护内存需求小的优势，我们需要利用一个octree_node的所有八个子节点是连续分配的特点，修改相关结构体的定义：

struct voxel_pos
{
	uint32 x:21;
	uint32 y:21;
	uint32 z:21;
};
struct octree_node
{
	uint32 first_child: 28;
	uint8 x_diff:1;
	uint8 y_diff:1;
	uint8 z_diff:1;
	uint8 is_full_block:1;
};
struct first_child_info
{
	voxel_pos pos;
	uint32 parent;
};
struct octree_layer
{
	uint32 layer_index;
	float voxel_length;
	std::vector<octree_node> nodes;
	std::vector<first_child_info> first_child_infos;
};

这里每个octree_node不再存储其体素的(x,y,z)坐标，而是存储其体素坐标相对于其父节点的第一个子节点的体素坐标的差异值。此时第一个子节点的体素位于这八个连续子节点所代表的2*2*2立方体的最低点，其他的七个点与first_child的体素坐标差异在三个轴上最大值都是1，所以这里我们用x_diff,y_diff,z_diff三个bit来存储。同时八个子节点的排列方式按照(x_diff * 4 + y_diff*2 + z_diff)递增的顺序，这样获取了任意一个octree_node的指针A之后都可以通过A-(A->x_diff * 4 + A->y_diff*2 + A->z_diff)的形式来获取这八个连续子节点的第一个节点的指针，进而可以获得第一个节点在nodes中的索引。对于每个作为first_child的octree_node都在对应octree_layer::first_child_infos里有一个元素来存储他的完整体素坐标和父节点的偏移。利用这些信息我们可以恢复之前定义在octree_node中的parent和(x,y,z)信息：

first_child_info octree_layer::get_first_child_of_parent(const octree_node* A) const
{
	auto first_child_of_A_parent = A-(A->x_diff * 4 + A->y_diff*2 + A->z_diff);
	auto first_child_idx = first_child_of_A_parent->nodes.data();
	return first_child_infos[first_child_idx/8];
}
uint32 octree_layer::get_node_parent(const octree_node* A) const
{
	return get_first_child_of_parent(A).parent;
}

voxel_pos octree_layer::get_node_pos(const octree_node* A) const
{
	auto first_child_pos = get_first_child_of_parent(A).pos;
	first_child_pos.x += A->x;
	first_child_pos.y += A->y;
	first_child_pos.z += A->z;
	return first_child_pos;
}

通过这样的优化，每个octree_node只需要占用4个字节，再平摊一下first_child_infos的开销，一个最底层的octree_node大概会引入6个字节的开销，相对于之前的16*8/7=18来说节省到了原来的1/3，这样相对于高度场来说降低了一半以上的内存消耗，继续保持了其内存占用上的优势。

搞定了内存存储结构之后，我们开始使用这个八叉树结构来使用A*搜索计算两点之间的连通路径。此时我们面临之前使用稀疏高度场同样的问题：给定一个体素坐标(x,y,z)，如果获取其对应的octree_node和对应的octree_layer。这里我们可以利用八叉树的节点性质来自顶向下查询，为了让代码更简洁我们使用第一个版本的结构体定义：

std::pair<const octree_layer*, const octree_node*> octree::get_node(uint32 x, uint32 y, uint32 z) const
{
	auto total_layer = m_layers.size();
	vector<uint8> offsets;
	while(total_layer > 0)
	{
		uint8 temp_offset = (x%2) * 4 + (y%2) * 2 + (z%2);
		x>>=1;
		y>>=1;
		z>>=1;
		offsets.push_back(temp_offset);
		total_layer--;
	}
	uint32 first_child_offset = 0;
	uint32 query_layer = m_layers.size();
	while(!offsets.empty())
	{
		auto temp_offset = offsets.back();
		offsets.pop_back();
		const octree_node* cur_node = layers[query_layer].nodes[first_child_offset + temp_offset];
		if(cur_node->first_child == std::numeric_limits<uint32>::max())
		{
			return make_pair(&layers[query_layer], cur_node);
		}
		first_child_offset = cur_node->first_child;
		query_layer--;
	}
	assert(false);
}

如果我们在排列octree_layer::nodes的时候按照octree_node对应体素坐标的递增序，则对nodes做二分查询即可获取一个体素坐标对应的octree_node，不过此时需要先查询最底层的layer，当查询不到时再递归向上查询。如果采取了节省内存的第二个版本结构体定义的话，我们可以使用first_child_infos来进行二分查询，因为first_child_infos也是按照voxel_pos增长序排列的。

解决了voxel_pos到octree_node的映射之后，我们也顺带解决如何获取一个octree_node的六个方向邻居的问题，不过这里获取邻居节点又有其特殊性，如果某个方向邻居节点是有子节点的，我们需要获取当前邻居节点所有层级的子节点中全连通且与当前节点连接的子节点，这里我们需要一个函数来快速的判定两个带layer信息的voxel_pos对应的体素是否直接邻接：

// 计算一个voxel pos在上一层layer中父节点对应的voxel_pos
void voxel_pos::to_parent()
{
	x = x>>1;
	y = y>>1;
	z = z>>1;
}

bool is_voxel_pos_linked(uint32 layer_a, voxel_pos pos_a, uint32 layer_b, voxel_pos b)
{
	if(layer_a < layer_b)
	{
		swap(layer_a, layer_b);
		swap(pos_a, pos_b);
	}
	while(layer_a != layer_b)
	{
		b.to_parent();
		layer_b++;
	}
	// 在同一层级上的两个节点直接连接的条件是 x y z三个轴的差值有且只有一个是1
	int64 diff_value = 0;
	diff_value += abs(int64(pos_a.x) - pos_b.x);
	diff_value += abs(int64(pos_a.y) - pos_b.y);
	diff_value += abs(int64(pos_a.z) - pos_b.z);
	return diff_value == 1;
}

至此，A*搜索时的节点定位问题和邻居查找问题都解决了。

如果场景在轴上的体素个数大于4096，八叉树的内存需求又变得严峻起来。在一个包含了4096*4096*4096的三维空间中，假如xz平面的底面平铺一层阻挡体，即使使用压缩内存版本的结构体定义，八叉树的内存占用为4096*4096*2*6=192MB。考虑到以0.25cm作为体素单位长度的情况下，4096个体素对应的边长为1km，1km*1km*1km的场景需要这样的内存需求大小还是难以接受，特别是现在游戏场景的边长都超过8km，逐渐往16km狂奔。仔细分析一下每一层的节点内存信息，发现最底层的节点数量大约是其他所有层节点数量总和的7倍，而最底层的所有octree_node是没有子节点的，所以first_child字段是可以删除的。在压缩内存的结构体定义中删除占据28bit的字段导致只剩4bit，即可以进一步节省内存到原来的1/8，从而可以将总体内存消耗降低到1/4。基于这样的字段压缩思想，游戏界提出了稀疏八叉树SVO(Sparse Voxel Octree)。SVO在字段压缩上更为激进，他将原来底下三层数据的信息合并为一层特殊的leaf_layer，同时在leaf_layer中只存储uint64，每个uint64代表一个4*4*4的体素立方体里每个体素是否是阻挡体的信息，即一个体素只需要1bit来存储。此时稀疏八叉树的结构体定义如下：

struct leaf_node
{
	uint64 value;
};
struct voxel_pos
{
	uint32 x:21;
	uint32 y:21;
	uint32 z:21;
};
struct octree_node
{
	uint32 first_child: 28;
	uint8 x_diff:1;
	uint8 y_diff:1;
	uint8 z_diff:1;
	uint8 is_full_block:1;
};
struct first_child_info
{
	voxel_pos pos;
	uint32 parent;
};
struct octree_layer
{
	uint32 layer_index;
	float voxel_length;
	std::vector<octree_node> nodes;
	std::vector<first_child_info> first_child_infos;
};


struct svo_tree
{
	vector<octree_layer> layers;
	vector<leaf_node> leafs;
};

最底下一层的octree_layer里octree_node::first_child指向的是svo_tree::leafs里的偏移量。下面是一个图形化的结构示例：

在采用此结构来存储体素数据之后，在一个包含了4096*4096*4096的三维空间中，假如xz平面的底面平铺一层阻挡体，稀疏八叉树的内存占用为(4096/4)*(4096/4)*(8+5)=13MB，相对于之前的192MB简直妙手回春医学奇迹！不过这样的内存优化也有其劣势，即路径搜索获取一个节点的邻居时，如果遇到了最下面一层的layer，需要计算邻接当前节点的leaf_node对应面的16个体素是否可以直接连通。此外加入到OpenSet里的数据还要区分是正常的octree_node还是leaf_node。为了在搜索时对这两类node做统一存储，我们定义一个svo_link的结构：

struct svo_link
{
	int32 layer: 4; // 当前node所在的层级
	int32 node_offset: 22; // 当前node在对应层级的nodes里的索引
	int32 leaf_cube_offset: 6; // 如果layer为0 且node不是全阻挡或者全联通 则这六个bit代表对应的leaf_node value字段里的bit索引
};

由于A*搜索时如果遇到一个leaf_node需要考虑相邻的16个voxel对应的bit，最大会引入新的16个元素到OpenSet中，所以我们的启发函数最好加入一个对svo_link::layer的惩罚项，layer越小，惩罚越大。这样的启发函数设置会让路径优先使用更大粒度的octree_node，从而减少搜索时OpenSet的大小。

基于寻路网格的三维地表寻路

前面章节介绍的是一个可以六方向移动的单位如何在三维场景中使用体素数据进行寻路，可以用来解决空中寻路和水下寻路的问题。但是这种寻路方式与我们常见的游戏中的entity移动方式很不一样，常见的游戏中我们控制的角色和服务端创建的NPC都是只能在特定物体的表面进行寻路的，同时要求这些物体表面的斜率不能太大。为了解决这种最常见的地表寻路问题，我们首先需要解决如何定义三维空间中的可行走表面。例如我们可以继续利用之前定义的三维空间的高度场span体素数据，只使用可连通span的底面体素作为可行走表面，执行A*寻路时OpenSet中只支持span的底面体素。如果从span(A)的底面移动到span(B)底面面带来的体素高度差大于特定值，则认为这条连接斜率过大，不再具有连通性。加入这些限制之后，我们就可以继续用体素进行三维地表的寻路了。不过之前也提到了使用高度场会带来非常大的内存需求，1024*1024*1024的空场景都需要1024*1024*(12 + 4)=16MB的内存，在常规使用的人物地表移动所需的体素精度一般为25cm，此时16MB只能表示边长为256M的立方体区域，对于常规的2KM左右边长地图来说，所需的内存就会膨胀到160MB，完全不具有可行性。

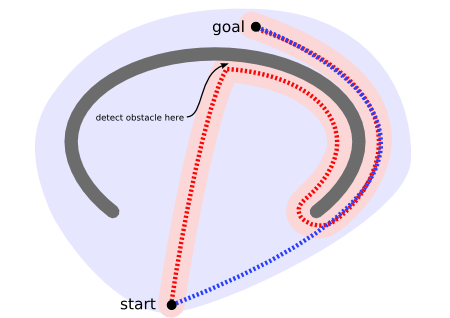
为了使用较少的内存来解决三维地表寻路的问题，研究人员提出了寻路网格NavMesh(Navigation Mesh)这样的数据结构。在NavMesh中，可行走地表区域不再使用体素来表示，而是使用多个凸多边形Convex Polygon来表示。如果两个凸多边形之间共享了一条边，则这两个凸多边形可以通过这条边进行连通。下图中就是一个使用NavMesh表示的地图可行走区域，绿色区域代表可行走区域，亮绿色的线段表示凸多边形的边，所使用的凸多边形为三角形：

从上图中可以看出，只需要三个点组成的三角形即可描述一块非常大的平坦开阔区域。对于一个完整的空正方形场景，仅需两个三角形即可描述全场景的寻路表面，相对于直接用体素span来描述这块可行走表面来说内存节省了很多。在实际使用中的1km*1km左右的地图中，其对应的NavMesh一般不会超过1M。正因为NavMesh在内存上的优势，导致现在基本所有的游戏引擎在寻路功能上都采用基于开源的RecastNavigation来构造三维空间的地表寻路NavMesh数据。

由于RecastNavigation作为寻路的基础解决方案的重要性，本书中后续将使用一整个章节去介绍RecastNavigation的原理细节，下面将只简要介绍一下如何在二维场景中构造NavMesh的基本流程。

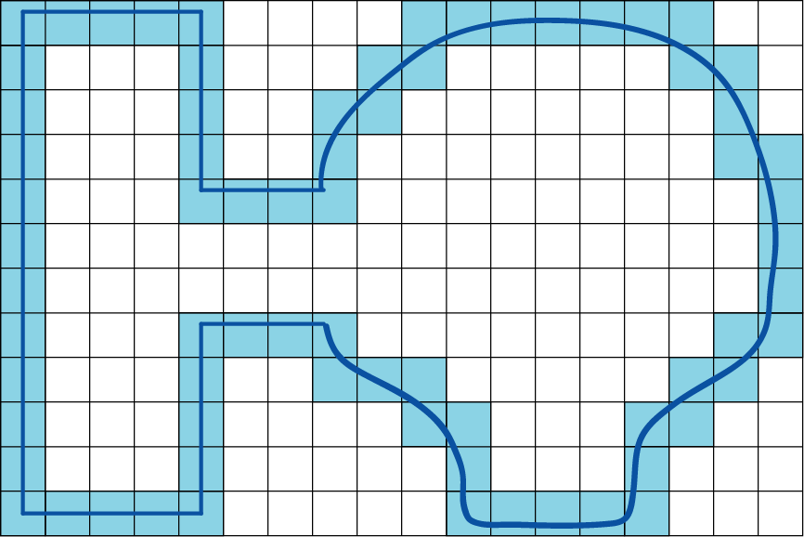
在二维场景中构造NavMesh我们依然需要以来grid数据，我们用特定粒度的正方形网格对地图grid进行采样，来标记grid中的可行走区域和不可行走区域。在下图中我们用一条首尾相连的曲线来描述可行走区域的边缘：

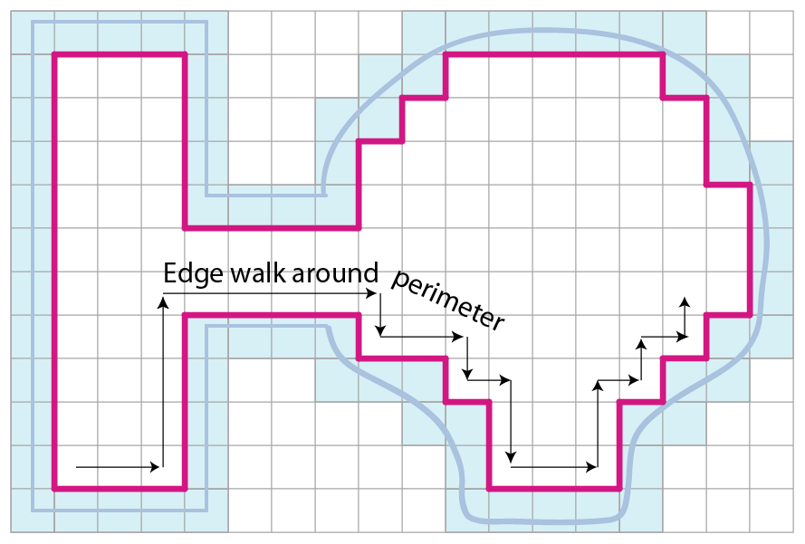
有了整个grid数据之后，我们获取整个可行走区域的内测边缘，获取一个连通线段组成的回路：

由于按照坐标轴构造的线段过于曲折，接下来按照一定的规则删除部分不必要的端点，构造一个形状基本相似的简化多边形：

有了这个简化多边形之后，下一步需要将简化多边形切分为多个凸多边形，这里最经典的方法是使用Delaunay方法进行三角形划分。不过我们这里并不要求切分为三角形，所以采用一个基于贪心的方法。遍历每个点A，获取多边形中对应最近的点B，如果(A,B)不是一条现有的线段，则将线段加入到待处理优先队列，其优先级与线段的长度除以两点之间相连之前最短路径的长度的比值相关，比值越小，优先级越大：

利用上述规则，构造一个多边形处理队列，初始时将原始多边形放入其中。每次从队列中拿出一个多边形，如果此多边形不是凸多边形，则获取最优分割边将此多边形切分为两个子多边形，并加入到多边形处理队列中。不断处理直到队列为空，最终形成了下图：

上述方法只处理了可行走区域内无阻挡区域的情况，对于有阻挡区域时，对阻挡区域的多边形里的每个点都找到场景中离其最近且原本不连通的点，如果不是已经有的边且不与现有的所有边交叉则构造新边，边的添加优先级与边的长度成反比：

如果新添加的边形成了一个新的连通多边形，且不是凸多边形，则递归进行处理，最终得到了这样的结果：

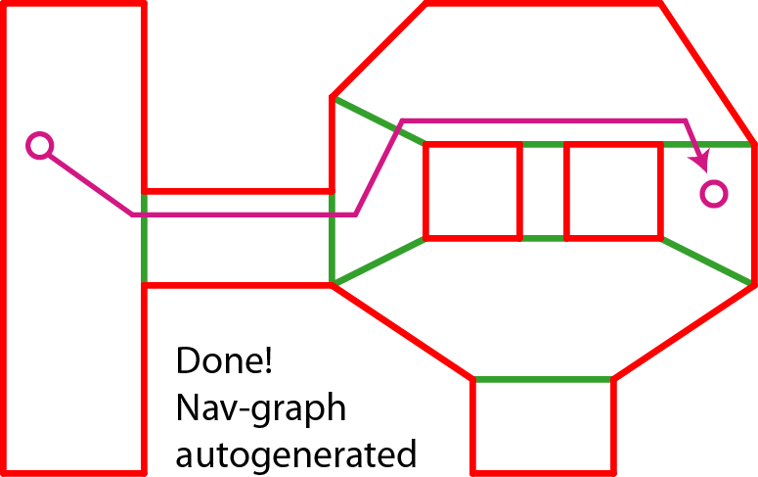
这样我们就得到了一个包含了阻挡体的NavMesh，流程看上去很简单但是其实很多细节在里面。更多的细节将在后面介绍RecastNavigation的章节中进行提及，自此我们将认为从原始地图生成NavMesh是一个已经解决了的问题。

在拥有了描述场景地表数据的NavMesh之后，用这个数据来执行点与点之间寻路的流程替换成了凸多边形之间的路径搜索。不过这里我们首先需要解决如何查找点所对应的凸多边形。

判断点在是否在凸多边形内的算法是确定的，在凸多边形的顶点按照逆时针排列成为P(0),P(1)...P(n)的时候，检查目标点P是否在所有的P(a)->P(a+1)直线直线的同一边，如果都在同一边则认为此点在凸多边形内。这里判断是否在同一边就是计算向量P(a)->P 与向量P(a)->P(a+1)的叉积的值的正负性是否不变， 如果正负性发生改变则认为不在凸多边形内。

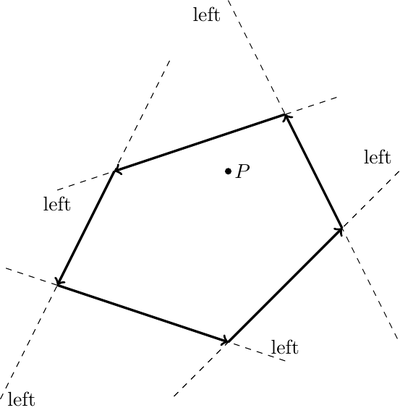
bool IsInConvexPolygon(Point testPoint, vector<Point> polygon)
{
    //Check if a triangle or higher n-gon
    Debug.Assert(polygon.size() >= 3);

    //n>2 Keep track of cross product sign changes
    auto pos = 0;
    auto neg = 0;

    for (auto i = 0; i < polygon.size(); i++)
    {
        //If point is in the polygon
        if (polygon[i] == testPoint)
            return true;

        //Form a segment between the i'th point
        auto x1 = polygon[i].X;
        auto y1 = polygon[i].Y;

        //And the i+1'th, or if i is the last, with the first point
        auto i2 = (i+1)%polygon.Count;

        auto x2 = polygon[i2].X;
        auto y2 = polygon[i2].Y;

        auto x = testPoint.X;
        auto y = testPoint.Y;

        //Compute the cross product
        auto d = (x - x1)*(y2 - y1) - (y - y1)*(x2 - x1);

        if (d > 0) pos++;
        if (d < 0) neg++;

        //If the sign changes, then point is outside
        if (pos > 0 && neg > 0)
            return false;
    }

    //If no change in direction, then on same side of all segments, and thus inside
    return true;
}

有了这个判定方法之后，我们可以通过遍历NavMesh内的所有凸多边形执行上述函数来获取目标点所在的凸多边形，但是这样做的话效率太低了。我们需要一个更加快速的查询结构来应对静态Mesh场景中点对应的凸多边形查询，游戏中经常用层次包围体BVH(Bounding Volume Hierachy)这样的结构。所谓包围体Bounding Volume就是一个可以将任意几何体包围的简单形状，常见的包围形状包括轴对齐包围盒（axis-aligned bounding box，AABB 包围盒）、包围球（bounding sphere）以及定向包容盒子（Oriented Bounding Box,OBB）等。为了实现上讨论简单我们这里只使用AABB的包围盒，因为计算时只需要获取多边形内所有点在所有轴的最大最小值即可。

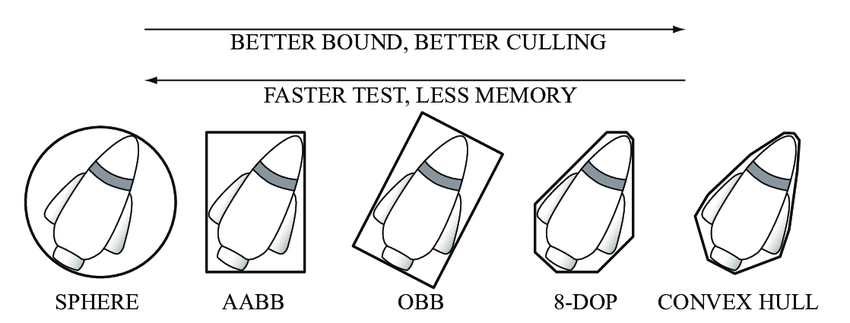
所谓的层次包围体技术 指的是将所有包围体分层逐次地再次包围，获得一个更大的包围体，直到包围住所有物 体。

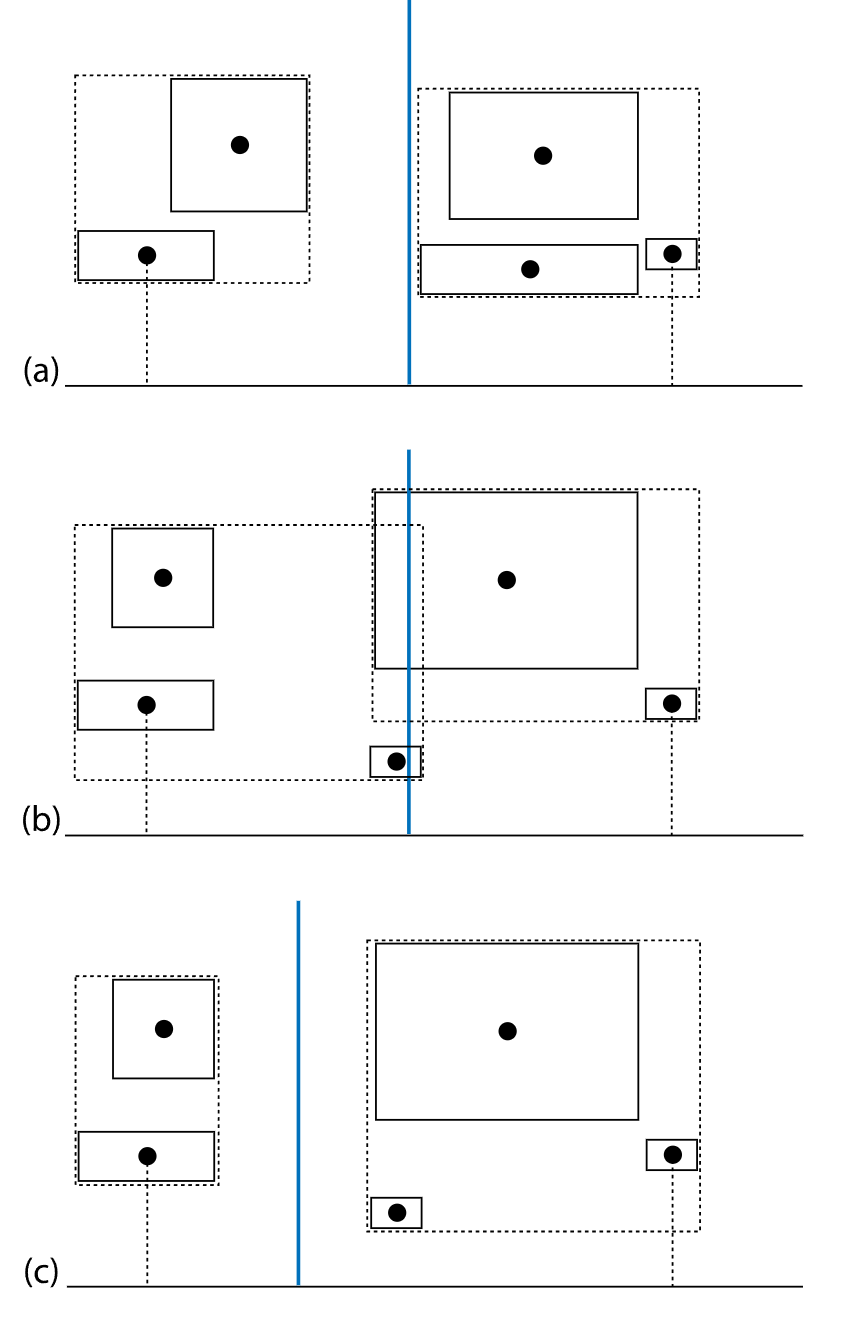
构建BVH树的算法比较简单，采用的是一个自顶而下的树形构建方法：

1. 初始时构造一个节点，节点内包含所有的多边形，
2. 然后选用一条与轴平行的直线，将所有的多边形按照多边形包围盒中点在直线的左右侧进行分割，生成左侧多边形集合和右侧多边形集合，
3. 分别构造左右子树对应这两个集合并递归的进行BVH构建，直到集合内多边形数量大小小于特定值（例如5）。
4. 构造完成之后，每个叶子节点计算其内部的所有多边形的包围盒的并集，作为此叶子的包围盒大小
5. 每个非叶子节点的包围盒为两个子节点的包围盒的并集

上述算法的核心就是如何在步骤2中选取一条合适的与轴平行的直线，使得两个子树的大小均衡。实践中会采用这样的方法来选取：

1. 首先获取节点对应的多边形集合在各个轴上所占据的区间的并集，计算轴上覆盖的长度，选取覆盖长度最长的轴
2. 获取节点对应的多边形集合的包围体中心坐标在所选取的轴上的投影值集合，获取其中的中位数作为结果直线的坐标值

第一步的耗时与多边形数量成简单线性关系，第二步的计算可以直接使用std::nth_element来计算中位数，时间复杂度也是多边形数量的简单线性。所以自顶向下构造BVH的时间复杂度类似与快速排序的时间复杂度。对于静态场景的离线计算来说这样的时间复杂度是非常优秀的，而且其占用的内存只是原始多边形数据的几分之一。

有了BVH之后我们就可以快速的进行查询点所在的凸多边形了：

1. 首先构造一个节点队列，将BVH根节点放入队列中
2. 每次从队列中POP一个节点，检查目标点是否在此节点的包围盒中，如果在包围盒内
   1. 如果当前节点不是叶子节点，则将当前节点的两个叶子节点放入节点队列等待后续处理
   2. 如果当前节点是叶子节点，遍历当前叶子节点内存储的凸多边形列表，使用凸包算法判定点是否在凸多边形内，如果在则作为结果返回
3. 如果队列为空 则代表节点无对应的凸多边形

整体流程就是一个二叉树的递归下降流程，不过这里又有点不同，因为一个节点的左右两个子节点都可能会进入处理。所以查询的最优时间复杂度等价于树高，最坏时等价于整体多边形集合的大小，不过正常情况下的执行时间跟最优复杂度差不多。如果想构造更为均衡的BVH树来执行查询，可以参考使用基于表面积启发SAH((Surface Area Heuristic)的划分方法，具体细节参考PBRT的关于BVH的内容

解决了获取点对应的凸多边形这个问题之后，使用NavMesh计算寻路就是在计算凸多边形的连通路径。这里可以继续使用我们在A*搜索上的相关经验，不过在最终的路径生成时还需要结合NavMesh自身的一些特性来做优化。以下图中的NavMesh为例，我们要执行一次从C1到C8的连通路径查询：

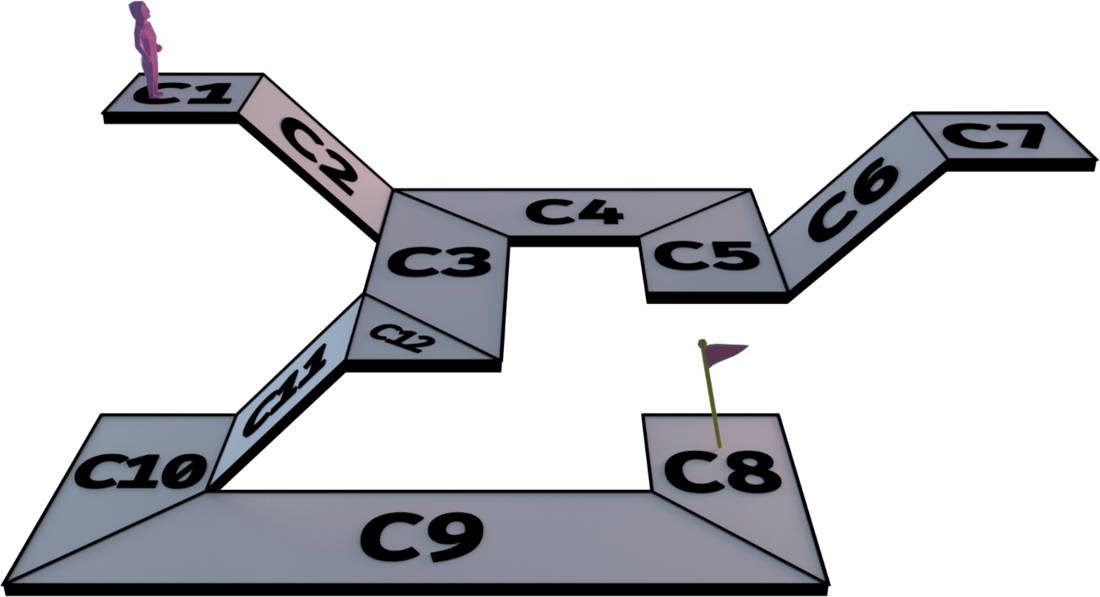
根据共享边决定的凸多边形连通性，我们可以获得下面的这个红色多边形路径：

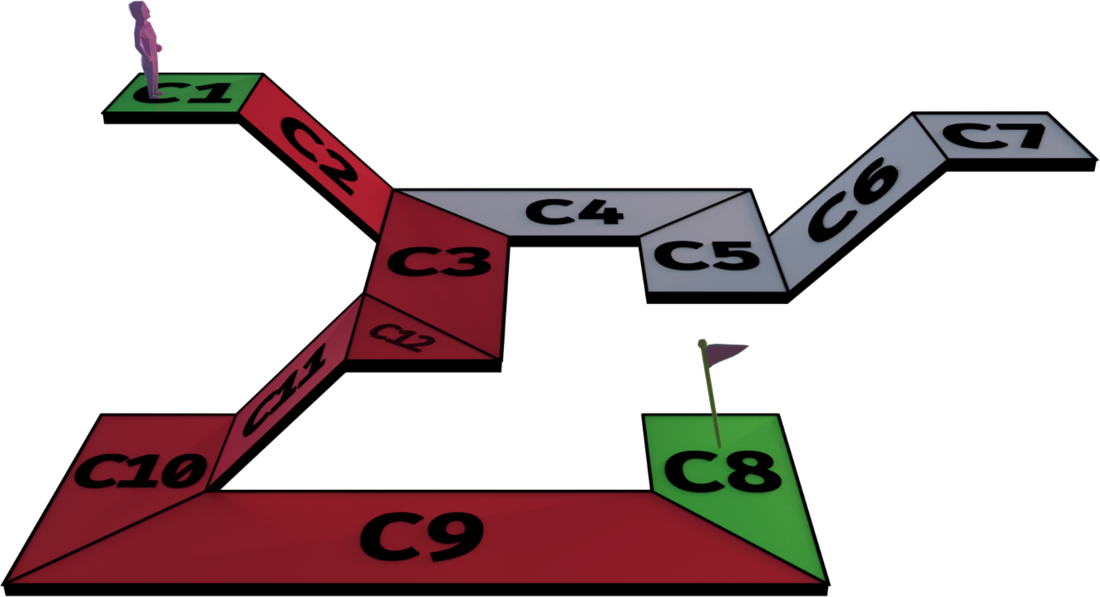
获取多边形路径之后我们获取相邻的两个多边形所共享的边，如下图中的粉色线段所示：

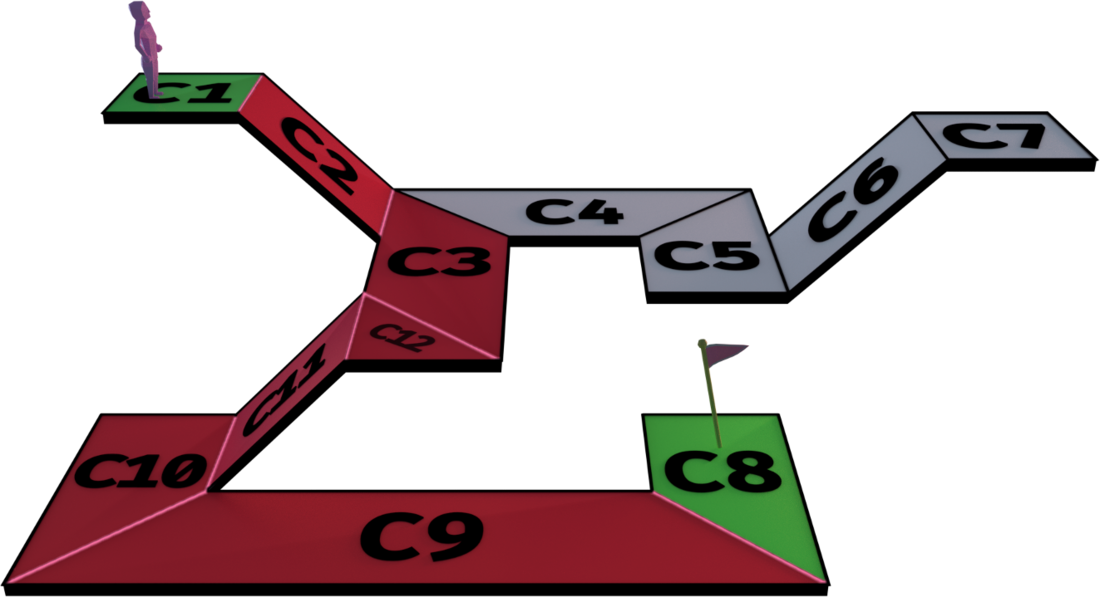
有了这些边之后我们可以很方便的构造出由线段组成的路径：选取每个多边形在连通路径上的两个共享边，将两条边的中点进行连接，并将起点和终点拼接到首尾，最终形成了下图中的橙色路径。

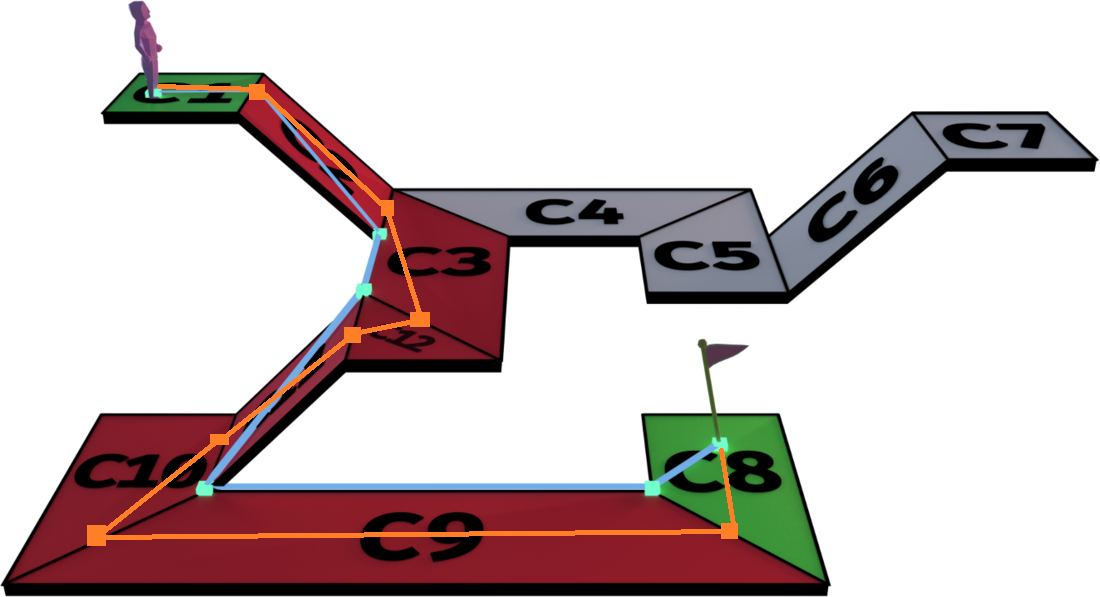
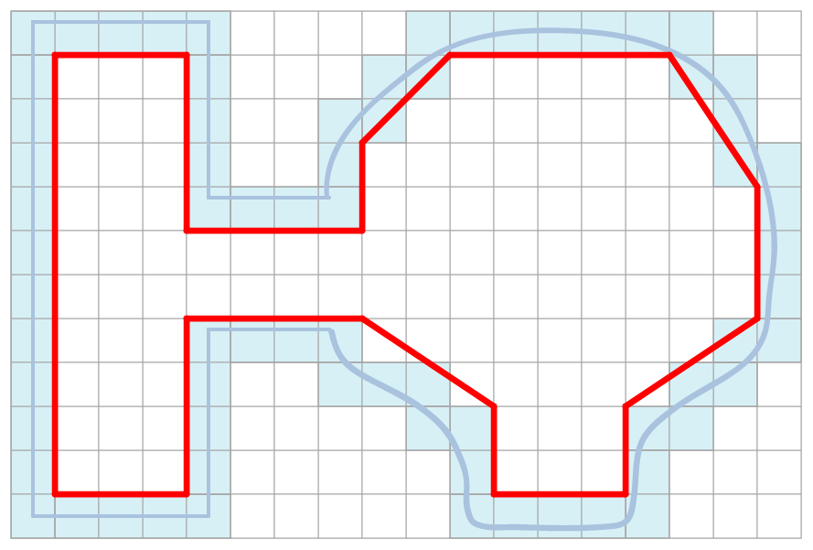
但是我们观察上图发现，浅蓝色路径也是一条通过多边形路径的线段路径，同时这条路径的总长度比黄色路径短很多。事实上经过首尾两点并通过指定多边形列表的线段路径有很多条，例如将多边形的重心连接起来也是一条满足需求的路径。为了找到连通两点并经过指定连通多边形路径的最短线段路径，我们需要使用拉绳算法。这个算法执行的是一个贪心过程，算法目标是计算出路径中所有的拐点，也就是线段之间的连接点。我们的目的是尽可能的减少拐点，以达到路径平滑同时路径最短的目的。算法的具体流程见下图：

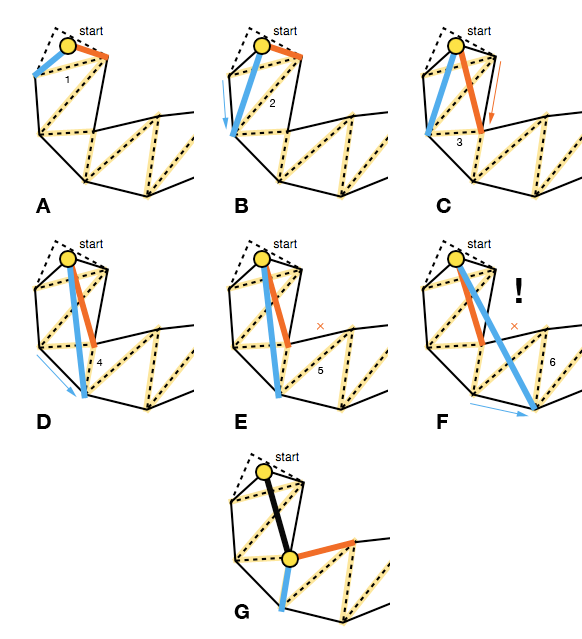
初始的时候我们需要如下参数：

1. start 作为寻路的起点

2. left,right 作为中间临时变量 他们与start围成的三角形记录可行走区域

3. polys记录剩下的还未探索的多边形

初始时可以把left right 设置为第一个Poly边上的两点， 即A图。接下来，需要依次移动左右两条边，按顺序处理路径上的Poly。每次遇到一条新的边，考察这个边的left2 right2与start之间的连线与原来的left right线段之间的关系。其实left2 right2总是会有一个点与left right重合，所以只需要考虑新加入的节点即可。

1. 如果新加入的节点与start之间的线段与原来的left->right线段相交，则更新left right为left2, right2，即缩小可行走三角形区域 如上图中的B, C,D

2. 不相交的话，我们需要将left right里与left2 right2重合的点设置为拐点，加入到拐点路径里， 然后将这个点当作新的start，下一条Poly边的left right作为新的left right，一路迭代下去， 如图F G

整个算法一路迭代，处理了最后一个多边形之后，判断最后一个拐点是否在此多边形与终点所在的多边形共享边上：

1. 如果在共享边上，则直接拼接终点到已经计算出来的路径之后作为最后的起点到终点之间的连通路径。
2. 如果不在共享边上，
   1. 如果最后一个拐点与终点之间的线段不会离开连通路径中的多边形，则直接把终点加入到拐点最后，生成一条连通路径
   2. 如果连线会离开连通路径中的多边形，则选择拐点经共享边两个端点连接到终点的这两条路径中的长度最小者，作为最后的拐点，并把终点拼接到最后，生成一条连通路径

对于三维场景中的凸多边形列表，我们可以将这些凸多边形都投影到xz平面，再执行上述算法。获取平面路径之后，再计算这条路径与平面投影共享边相交的点，将这些点转换为三维平面对应共享边的点之后，插入到原有路径中，即可获取三维场景中拉绳算法计算出的最短路径。