游戏中的随机
游戏中的很多系统会使用随机性来构造更加丰富的游戏体验。由于随机结果是无法预测的,所以随机判定发生了那种远超玩家预期的结果时会给玩家带来一些值得记忆与分享的惊喜时刻。其中随机性特性最明显的场景主要有如下两类:
- 依据指定概率触发某种事件,攻击触发暴击、被动晕就是这种。打过
Dota的玩家想必都体验过白牛无限晕、蓝胖四倍点金的快乐:
在暗黑破坏神2中刷了几十年的的玩家想必都知道满变量悔恨的含金量:

- 依据指定权重分布来生成某种物品道具,玩家常说的开宝箱就是这种。但是一般来说这些随机事件的概率都不是很高,所以大部分时候玩家对于这种随机性感受到的体验都比较负面。这种概率过低的随机造成了无数个玩家即使在暗黑破坏神2中游荡了几十年依然没有收集齐所有的符文,并在阴阳师大火的时候获得了“非酋”这一专属荣誉称号。各位“非酋”也试图在游戏内表演斋戒焚香沐浴更衣等各种行为艺术来试图增加这些物品的掉落概率,这也就造成了游戏界口口相传的一句话:
玄不救非, 氪不改命
在受到无数玩家的口诛笔伐之后,最终相关监管部门提出了游戏公司必须提前公布随机掉落概率这一规定。不过这种公布概率的规定也并没有抚平各位“非酋”心中的创伤,也没有扭转他们之前的各种玄学行为。
为此本章就来介绍一下游戏内对于这两种随机机制的具体实现,来解答玩家对这种随机性的疑惑。
依概率触发
依概率触发事件这种随机模式最广为人知的场景就是攻击时判定是否触发暴击、闪避、眩晕等这些特殊攻击效果,由于这些随机事件的概率一般都是在5%以上,所以玩家对于这种随机事件都是喜闻乐见。这种随机事件的判定计算也比较简单,利用随机数生成器生成一个[0,1]之间的浮点数a,然后与指定的发生概率b做比较,如果a>=b则代表这个随机事件判定通过可以发生。
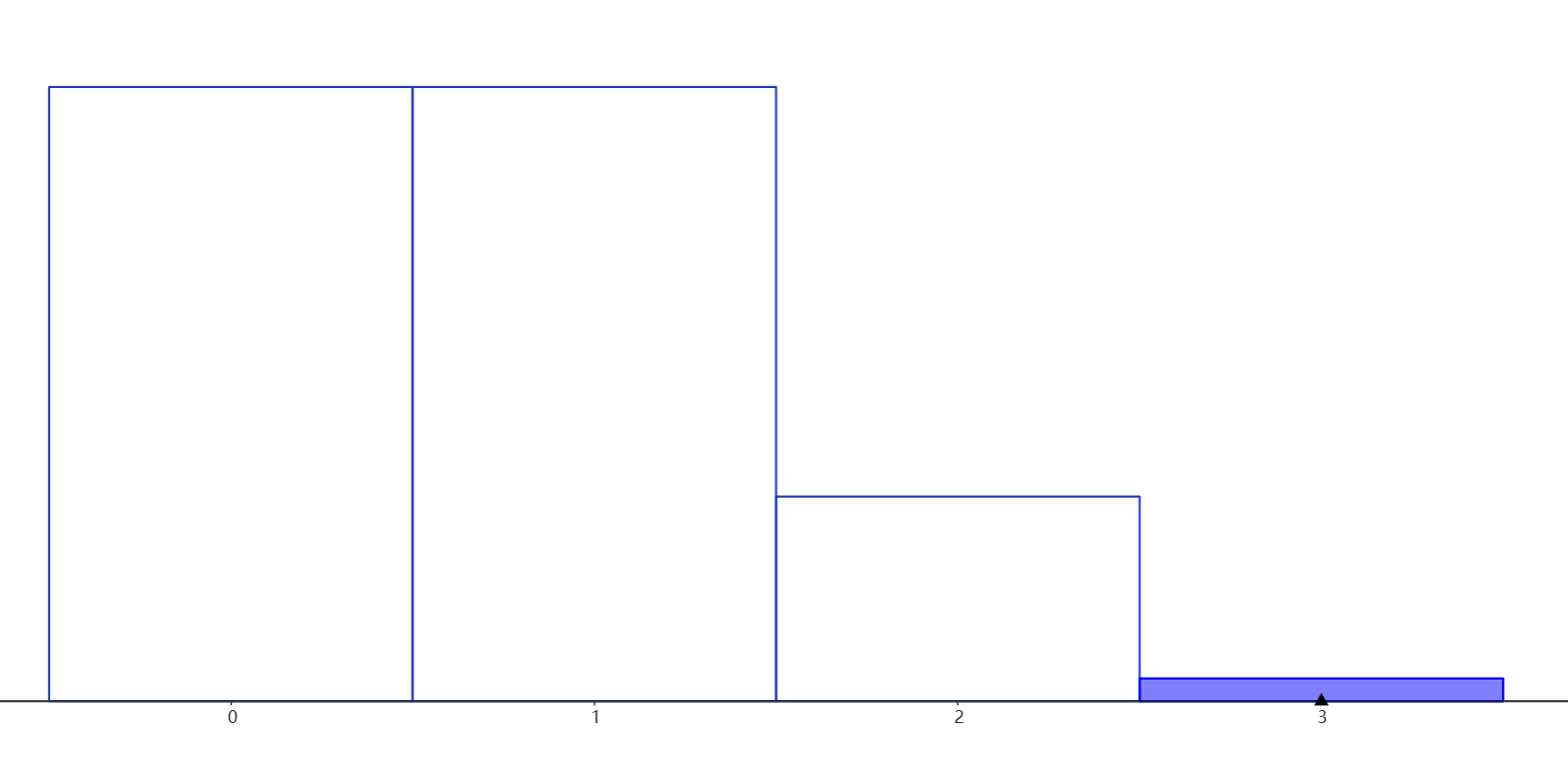
虽然这种简单的实现虽然是正确的,但是由于攻击判定的频率比较高,可以达到一秒多次,每次随机判定之间毫无关系,这样就很容易出现短时间内若干的连续不触发或者连续的触发这种现象,也就是Dota玩家常说的“欧洲晕锤”与“非洲晕锤”。假设攻击时有25%的概率触发被动晕,则连续三次攻击中触发被动晕的次数呈如下分布,三次都触发眩晕的概率为0.0156:
这样的分布还是比较符合玩家直觉的,我们考虑进一步把攻击次数扩大到100,此时再来看一下触发次数的概率分布:
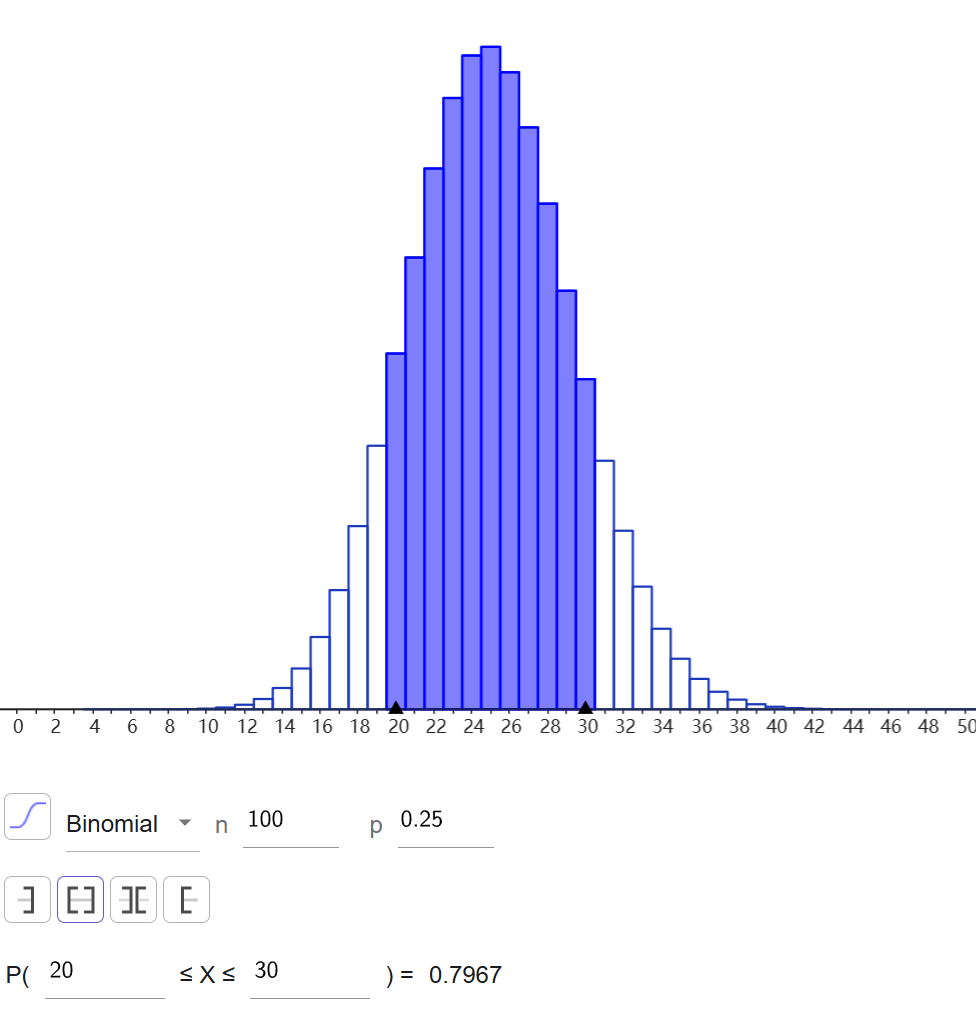
可以看出触发次数在[20,30]区间内的概率为0.8,在这个区间之外的概率仍然比较大超过0.2,连续10次没有触发的概率为,这个值仍然比较大。这种随机事件的由于其相互独立的性质导致出现与平均概率比较大差异的情况仍然是比较常见的。这种概率偏差对于观赏性来说是一种佐料,但是对于游戏平衡性来说却是有害的。因为这种刀刀烈火、无限被动晕现象的出现非常明显的影响了游戏的后续结算结果。对于竞技游戏来说这种完全不可控的随机性是要想方设法避免的,所以Dota2 6.81版本中率先引入了反击螺旋随机触发的伪随机机制:
伪随机分布(pseudo-random distribution,简称PRD)在DotA中用来表示关于一些有一定几率的装备和技能的统计机制。在这种实现中,事件的几率会在每一次没有发生时增加,但作为补偿,第一次的几率较低。这使得效果的触发结果更加一致。
效果在上次成功触发后第N次测试中发生的几率(简称proc)成功触发的几率为。对于每一个没有成功触发的实例来说,PRD系统为下一次效果触发的几率增加一个常数C。该常数也会作为初始几率,比效果说明中的几率要低,并且是不可见的。一旦效果触发,这个计数器就会重置。
技术上,如果以表示第次事件发生, 表示事件不发生。伪随机分布使用。同样地,当时,如果事件一直没有发生,那么在满足中的最小次判定时,该事件必然发生。 事件必然发生。因此概率分布为:
用更通俗的文字来阐述伪随机的做法是这样的:
- 对于某个以概率
P触发的事件,计算出一个数值C,同时建立一个变量N来记录已经连续多少次没有触发 - 每次采样来计算触发时,使用的概率不是
P,而是(N+1)*Q, - 如果此次采样触发了这个事件,则将
N设置为0 - 如果此次采样没有触发这个事件,则将
N设置为N+1
总的来说就是随着连续不触发的次数增大对应的触发概率也增大,这样总会导致概率大于1,从而引发一次事件触发。下面就是碎颅锤的伪随机例子:
对近战英雄,碎颅锤的重击有
25%几率对目标造成眩晕。那么在第一次攻击时,实际上只有大约8.5%几率触发重击。随后每一次失败的触发会增加大约8.5%触发几率。于是到了第二次攻击,几率就变成大约17%,第三次大约25.5%,以此类推。在一次重击触发后,下一次攻击的触发几率又会重置到大约8.5%。那么经过一段时间之后,这些重击几率的平均值就会接近25%。
为了保证这个PRD算法的正确,我们需要为每个P计算出对应的C出来,这里需要用到牛顿二分法来做数值逼近:
// 这个函数计算给定的C时对应的P
double PfromC( double C )
{
double pProcOnN = 0;
double pProcByN = 0;
double sumNpProcOnN = 0;
int maxFails = (int)std::ceil( 1 / C );
for (int N = 1; N <= maxFails; ++N)
{
pProcOnN = std::min( 1, N * C ) * (1 - pProcByN);
pProcByN += pProcOnN;
sumNpProcOnN += N * pProcOnN;
}
return ( 1 / sumNpProcOnN );
}
// 下面这个函数使用二分法来逼近 直到由这个C计算出来的P与传入的P基本相等
double CfromP( double p )
{
double Cupper = p;
double Clower = 0;
double Cmid;
double p1;
double p2 = 1;
while(true)
{
Cmid = ( Cupper + Clower ) / 2;
p1 = PfromC( Cmid );
if ( std::abs( p1 - p2 ) <= 0 ) break;
if ( p1 > p )
{
Cupper = Cmid;
}
else
{
Clower = Cmid;
}
p2 = p1;
}
return Cmid;
}
每次去运行时计算这个C还是比较耗时的,幸运的是对于常见的概率已经有现成的表格可以查询到对应的C值:
| C | 通常几率 | C近似值 |
|---|---|---|
| 0.003801658303553139101756466 | 5% | 0.38% |
| 0.014745844781072675877050816 | 10% | 1.5% |
| 0.032220914373087674975117359 | 15% | 3.2% |
| 0.055704042949781851858398652 | 20% | 5.6% |
| 0.084744091852316990275274806 | 25% | 8.5% |
| 0.118949192725403987583755553 | 30% | 12% |
| 0.157983098125747077557540462 | 35% | 16% |
| 0.201547413607754017070679639 | 40% | 20% |
| 0.249306998440163189714677100 | 45% | 25% |
| 0.302103025348741965169160432 | 50% | 30% |
| 0.360397850933168697104686803 | 55% | 36% |
| 0.422649730810374235490851220 | 60% | 42% |
| 0.481125478337229174401911323 | 65% | 48% |
| 0.571428571428571428571428572 | 70% | 57% |
| 0.666666666666666666666666667 | 75% | 67% |
| 0.750000000000000000000000000 | 80% | 75% |
| 0.823529411764705882352941177 | 85% | 82% |
| 0.888888888888888888888888889 | 90% | 89% |
| 0.947368421052631578947368421 | 95% | 95% |
下面我们来使用程序来模拟C=0.085的时候统计触发所需次数,对应程序的代码在https://github.com/huangfeidian/random_util/blob/main/test/test_trigger_by_prob.cpp上,下面的是统计了100次触发的所需次数分布结果:
| 第N次才触发 | 出现次数 |
|---|---|
| 1 | 7 |
| 2 | 17 |
| 3 | 21 |
| 4 | 22 |
| 5 | 16 |
| 6 | 8 |
| 7 | 5 |
| 8 | 4 |
从这个表格中可以看出,触发所需次数大多在[2,5]区间内,比较平均,同时大于8次才触发的情况并没有出现。而且完成这100次触发所执行的采样次数为1*7+2*17+3*21+4*22+5*16+6*8+7*5+8*4=387,对应的触发概率为0.258,与目标值非常接近了。
基于PRD的效果连续多次触发或多次不触发是非常罕见的。这使得游戏的运气成分大大降低,在Dota 2中一个有那么多带几率的技能的世界中增加了一致性。
加权随机选择
加权随机选择(Weighted Random Choice)就是广大玩家深恶痛绝的开箱子玩法,打开宝箱玩家可以获取多种物品中的一个。单个宝箱中不同物品出现的概率由策划配置的出现权重来指定,在配表中会以这样的vector<pair<item_id, item_weight>>的形式存在,同时指定item_id为0的配置项对应本次宝箱结算不生成任何物品。对于这样的一个配置数组A,设total_weight为这个数组中所有元素的item_weight之和,则第i个item对应的随机获取概率为A[i].item_weight/total_weight。一般来说这里的item_weight类型就是uint32,所以这个宝箱结算问题也被成为离散加权随机选择。
这个问题最简单的解法就是生成一个[0, total_weight)之间的随机数A,然后顺序遍历这个权重数组并扣除每个元素对应的权重值B,直到A<B就返回当前遍历到的元素对应的item_id作为选择结果:
struct item_weight_config
{
std::uint32_t item_id;
std::uint32_t item_weight;
};
float uniform_random(float begin, float end); // 负责等概率的生成[begin, end)的一个随机数
item_id random_select_1(const vector<item_weight_config>& weights)
{
assert(weights.size());
std::uint32_t total_weight = 0;
for(const auto& one_weight_config:weights)
{
total_weight += one_weight_config.item_weight;
}
std::uint32_t temp_random_value = std::uint32_t(std::floor(uniform_random(0, total_weight)));
for(const auto& one_weight_config: weights)
{
if(temp_random_value <one_weight_config.item_weight)
{
return one_weight_config.item_id;
}
temp_random_value -= one_weight_config.item_weight;
}
return weights.back().item_id;
}
这个算法简明易懂,就是执行过程中有两次遍历,如果一个配置会被用来结算多次,则可以使用预先计算total_weight来避免这个值的重复计算:
struct select_context
{
vector<item_weight_config> weights;
std::uint32_t total_weight;
void init()
{
total_weight = 0;
for(const auto& one_weight_config:weights)
{
total_weight += one_weight_config.item_weight;
}
}
};
item_id random_select_2(const select_context& ctx)
{
assert(ctx.total_weight);
std::uint32_t temp_random_value = std::uint32_t(std::floor(uniform_random(0, ctx.total_weight)));
for(const auto& one_weight_config: ctx.weights)
{
if(temp_random_value <one_weight_config.item_weight)
{
return one_weight_config.item_id;
}
temp_random_value -= one_weight_config.item_weight;
}
return ctx.weights.back().item_id;
}
这样就可以将两次遍历降低到一次遍历,所需执行时间降低到原来的一半。在这个优化基础上,我们还可以通过预先计算前缀和来避免遍历时对temp_random_value的更新,进一步降低遍历时的工作量:
struct select_context
{
vector<item_weight_config> weights;
vector<std::uint32_t> sum_weights;
void init()
{
sum_weights.resize(weights.size());
std::uint32_t total_weight = 0;
for(std::uint32_t i = 0; i< weights.size(); i++)
{
total_weight += weights[i].item_weight;
sum_weights[i] = total_weight;
}
}
};
item_id random_select_3(const select_context& ctx)
{
assert(ctx.sum_weights.size());
std::uint32_t temp_random_value = std::uint32_t(std::floor(uniform_random(0, ctx.sum_weights.back())));
for(std::uint32_t i = 0; i< ctx.sum_weights.size(); i++)
{
if(temp_random_value <ctx.sum_weights[i])
{
return ctx.weights[i].item_id;
}
}
return ctx.weights.back().item_id;
}
这样在选择时的循环遍历只需要做一次比较操作即可。由于权重永远是正数,所以sum_weights数组肯定是一个递增的序列,我们可以利用这个性质使用二分查找来找到第一个大于temp_random_value的元素序号,以替代顺序遍历:
item_id random_select_4(const select_context& ctx)
{
assert(ctx.sum_weights.size());
std::uint32_t temp_random_value = std::uint32_t(std::floor(uniform_random(0, ctx.sum_weights.back())));
auto temp_iter = std::upper_bound(ctx.sum_weights.begin(), ctx.sum_weights.end(), temp_random_value);
return ctx.weights[std::distance(ctx.sum_weights.begin(), temp_iter)].item_id;
}
在这样的搜索实现下,预处理之外的复杂度从数组大小N降低到了log(N),在N>10时就可有显著提升。
log(N)复杂度的算法已经是非常高效了,但是这个复杂度其实并不是加权随机选择问题最终的王者,还存在一种预处理之外只需要常数时间即可获得选择结果的最优算法。不过在介绍这个最优算法之前,我们需要先了解一下这个算法最初的一个效率不怎么高的版本。
假设随机的权重数组为[[0,6],[1,4], [2,1], [3,1]],即道具[0,1,2,3]各自的权重为[6,4,1,1],这四个道具的随机概率为[1/2, 1/3, 1/12, 1/12],其柱状图如下:
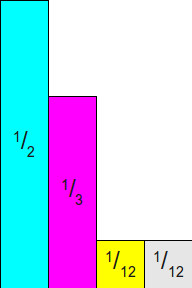
假设我们在上面图中的大矩形里随机选取一个点,所选点落入这四个柱形区域内的概率正比于这四个柱形的面积。由于是选点是均匀随机的,且柱形区域的底边长度一样高度等于随机概率,所以柱形区域的面积正比于其对应道具的随机概率。如果这个点在这四个带颜色的柱形区域内,则选择所在柱形对应的索引作为随机结果即可。但是上面图中右上角还有一大块区域是没有被柱形区域覆盖的,如果随机到的点在这个白色区域内,则需要再次随机,直到点落入到柱形区域内。采用这种随机选择方式,可以正确的依照权重来获取道具:
struct select_context
{
vector<item_weight_config> weights;
vector<float> relative_weights;
float p_max = 0;
void init()
{
relative_weights.resize(weights.size());
total_weight = 0;
for(std::uint32_t i = 0; i< weights.size(); i++)
{
total_weight += weights[i].item_weight;
}
for(std::uint32_t i = 0; i< weights.size(); i++)
{
relative_weights[i] = weights[i].item_weight * 1.0f/ total_weight;
p_max = std::max(p_max, relative_weights[i]);
}
}
};
item_id random_select_5(const select_context& ctx)
{
assert(ctx.weights.size());
while(true)
{
std::uint32_t random_index = std::uint32_t(std::floor((uniform_random(0, ctx.weights.size()))));
float random_weight = uniform_random(0, ctx.p_max);
if(random_weight <= ctx.relative_weights[random_index])
{
return ctx.weights[random_index].item_id;
}
}
}
在while循环内,单次循环体就可能得到最终的随机结果,这样成功的概率为所有柱形的面积除以最小包围矩形的面积,这个最小包围矩形的高度就是在init中计算的p_max,所以单次成功的概率为p=1/(n*p_max)。单次就成功只是理想情况,可能我们需要在while循环内执行多次才能获取随机选择结果,为了获取这个算法的复杂度我们需要计算while执行次数的期望。第k次才成功返回的概率为,所以总的次数期望为:
上面的后半部分可以转换为求,此时注意到:
将代入进入得到,所以最终的结果为:
所以期望执行的循环次数为n*p_max,这个的复杂度也是N的常数级别,比起前面介绍的二分查找慢了许多。
如果以某种机制来提高单次随机的成功概率p,则期望执行的循环次数会反比例的减小,当p被提升到1时,则只需要执行一次循环就可以获得随机选择的结果,接下来我们就来介绍如何通过巧妙的构造将p提升到1。
首先将前面的柱形分布图里所有的柱形高度都乘以n,这样会所有的柱形的面积累加值等于n,在这个缩放后的矩形里去随机选点等价于未缩放前:
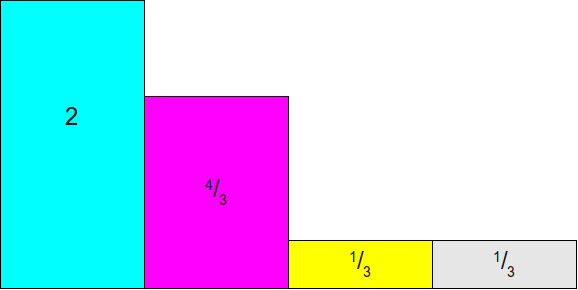
然后再以y=1画一条线,这条线与底边x轴构成的矩形面积等于n:
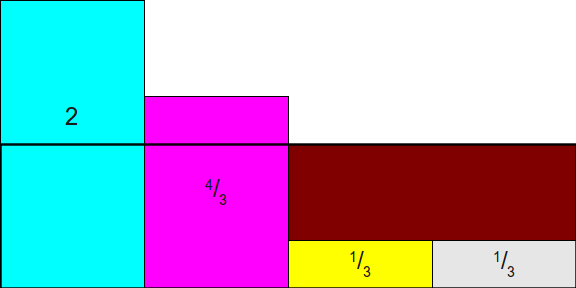
由于所有柱形的面积也等于n,所以可以通过某些切割机制将原来的柱形切分为多个小柱形,然后再拼接为前面辅助线构造的矩形。上图中的褐色区域就是需要填充的空间,而辅助线y=1上方的那些彩色柱形区域就是要切割掉的空间。
我们首先从面积为2的那个柱形中切分出一个2/3面积的部分,然后将这部分填充到最右方的1/3上面,剩下的图形如下:
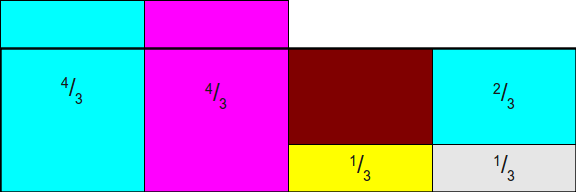
接下来继续从最左边剩下的4/3中切分出2/3给剩下的那个没有填充的1/3:
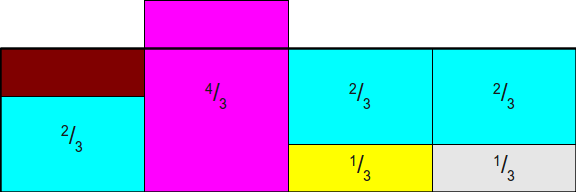
最后再从第二个柱形中切分出1/3给第一个柱形的剩下部分,这样就完成了柱形的切分再组装:

最后拼接出来的图形面积仍然是n,同时各个颜色的总面积等价于切分之前的总面积。但是此时已经不存在未被彩色柱形覆盖的区域了,所以在这个图形里随机选取一个点,计算出这个点对应的颜色,就可以获得随机选择的结果,不再需要多次抽样。就以上面的图来说,每个[k, k+1)区间内的小矩形数量最多为2,我们可以构造这样的一个数组来描述拼接的结构:
// 描述[k,k+1)的拼接信息
struct split_info
{
float self_prob = 0; // 每个小矩形的高度
uint32_t self_index = 0; // 每个小矩形的原始样本id
};
利用这个拼接数组,可以非常简单的单次随机即可计算出正确的结果:
uint32_t random_select_6(const std::vector<std::array<split_info, 2>>& rect_split_infos)
{
float temp_random_value = uniform_random(0, rect_split_infos.size());
uint32_t base_index = uint32_t(std::floor(temp_random_value));
float remain_random_value = temp_random_value - base_index;
if(remain_random_value <= rect_split_infos[base_index][0].self_prob)
{
return rect_split_infos[base_index][0].self_index;
}
else
{
return rect_split_infos[base_index][1].self_index;
}
}
上面的图里每个[k, k+1)区间内的小矩形数量最多为2目前来说只是一个特例,如果我们无法保证小矩形数量最多为2,上面的array<split_info, 2>要被替换为vector<split_info>,此时随机的实现就会变得不怎么高效了:
uint32_t random_select_7(const std::vector<std::vector<split_info>>& rect_split_infos)
{
float temp_random_value = uniform_random(0, rect_split_infos.size());
uint32_t base_index = uint32_t(std::floor(temp_random_value));
float remain_random_value = temp_random_value - base_index;
for(const auto& one_split_info: rect_split_infos[base_index])
{
if(remain_random_value <= one_split_info.self_prob)
{
return one_split_info.self_index;
}
remain_random_value -= one_split_info.self_prob;
}
}
这样的实现导致算法最坏执行时间被次级vector的最大容量所决定,对于这个最大容量我们唯一知道的信息是不会大于样本数量n,所以此时这个算法的复杂度仍然是样本数量n的线性复杂度。但是看前面介绍的简单样例只需要单次判断即可获得结果,如果有一种划分方法能保证最大容量为2的话,这个算法就只有常数时间复杂度,这样的最优情况非常吸引人。幸运的是我们可以证明存在这样的最大容量为2的划分,首先我们需要形式化的定义这个命题:
存在对于一个容量为n的vector<float> A, 如果accumulate(A.begin(), A.end(), 0) == A.size()且A中任意元素都大于0, 则存在一个std::vector<std::array<split_info, 2>> B,使得B.size()==n,且对于区间内[0, n)任意整数i,下面的条件都成立:
B[i][0].self_prob + B[i][1].self_prob == 1B[i][0].self_prob >=0 && B[i][1].self_prob >=0- 遍历
B中的每个元素C,再遍历C中的每个元素D,如果D.self_index==i,则累加D.self_prob,最后得到的累加值等于A[i]
这样的B就是我们所期望的最大容量为2的重整切割划分。接下来我们使用数学归纳法来证明对于上面的命题对于任意的正整数n都成立:
-
当样本数量为
1时,不需要执行切分合并,直接B[0][0].self_prob=1, B[0][0].self_index, B[0][1]={0,0}就可以满足需求,所以这个命题在n=1的时候成立。 -
假设对于样本数量为
k-1的A总是存在对应的B作为其最大容量为2的重整切割划分。当样本数量为k的时候,我们总是可以从A中选择两个索引i,j,使得A[i]>=A[j]且A[i]>=1>=A[j],此时从A[i]中切分一部分1-A[j]并填充到A[j]上,也就是B[j][0]={A[j],j}, B[j][1]={1-A[j], i},然后A[i]-=1-A[j], A[j]=1, swap(A[j], A.back()), swap(B[j], B.back())。此时我们将A[0],...A[k-2]构造为一个新的数组A2,将B[0],...B[k-2]构造出新的数组B2,这两个数组的大小为k-1。由于之前我们证明了对于n=k-1的时候总是存在一个B2是A2的重整切割划分,所以B2把里面的为j的self_index都重新赋值为k-1,然后再赋值到B[0],...B[k-2],此时的B也是对于原始A的最大容量为2的重整切割划分,即命题在n=k的时候也是成立。
上面的数学归纳法证明了对于任意的分布A我们总是可以构造一个最大容量为2的重整切割划分B,但是这里的构造算法不是很高效。每次缩减样本空间都需要扫描整个A数组来获取合符条件的两个索引i,j。下面我们来提出一种高效的算法来从A构造出B,这个构造方法可以避免每次扫描整个数组:
- 首先从
A数组构造两个新数组vector<pair<uint32_t, float>> C,D,C中存储原来高度大于1的所有元素的索引和高度,D中存储原来高度小于等于1的所有元素的索引和高度 - 每次从
D的末尾弹出一个元素E,- 如果
E.second==1,则代表此时不需要其他样本进行切分,执行B[E.first][0] = {E.first, E.second} - 如果
E.second<1,此时从C获取末尾元素F,从F中切除一部分1-E.second,使得E.first对应的区域被填充为1,以这个切分去构造B[E.first]
- 如果
- 判断
F.second是否小于等于1,如果小于等于1则将F从C的末尾转移到D的末尾 - 如果
D不为空,则回溯到步骤2再次执行;如果D为空,返回B作为结果。
下面的就是上述过程的cpp代码描述:
struct select_context
{
vector<item_weight_config> weights;
vector<std::array<split_info, 2>> rect_split_infos;
void init()
{
rect_split_infos.resize(weights.size());
std::vector<std::pair<uint32_t, float>> weights_gt_1;
std::vector<std::pair<uint32_t, float>> weights_le_1;
std::uint32_t total_weight = 0;
for(std::uint32_t i = 0; i< weights.size(); i++)
{
total_weight += weights[i].item_weight;
}
for(std::uint32_t i = 0; i< weights.size(); i++) // 对应步骤1
{
float relative_weight = weights.size() * weights[i].item_weight * 1.0f/ total_weight;
if(relative_weight > 1)
{
weights_gt_1.push_back(make_pair(i, relative_weight));
}
else
{
weights_le_1.push_back(make_pair(i, relative_weight));
}
}
while(!weights_le_1.empty()) // 对应步骤2
{
auto temp_le_1_back = weights_le_1.back();
weights_le_1.pop_back();
if(temp_le_1_back.second == 1) // 已经是1了 不需要再处理填充
{
rect_split_infos[temp_le_1_back.first][0].self_index = temp_le_1_back.first;
rect_split_infos[temp_le_1_back.first][0].self_prob = temp_le_1_back.second;
continue;
}
assert(!weights_gt_1.empty());
auto& temp_gt_1_back = weights_gt_1.back();
rect_split_infos[temp_le_1_back.first][0].self_index = temp_le_1_back.first;
rect_split_infos[temp_le_1_back.first][0].self_prob = temp_le_1_back.second;
rect_split_infos[temp_le_1_back.first][1].self_index = temp_gt_1_back.first;
rect_split_infos[temp_le_1_back.first][1].self_prob = 1- temp_le_1_back.second;
temp_gt_1_back.second -= 1 - temp_le_1_back.second;
if(temp_gt_1_back.second < 1) // 对应步骤3
{
weights_le_1.push_back(temp_gt_1_back);
weights_gt_1.pop_back();
}
}
}
};
上面的代码里有三个循环,每个循环的最大次数都被原始的输入数组大小限制住了,所以这个初始化流程相当于遍历了三次原始输入数组,其总时间复杂度为输入的线性复杂度。有了这个构造好的rect_split_infos之后,获取一个随机选择的值就很简单了:
uint32_t random_select_8(const select_context& ctx)
{
float temp_random_value = uniform_random(0, ctx.rect_split_infos.size());
uint32_t base_index = uint32_t(std::floor(temp_random_value));
float remain_random_value = temp_random_value - base_index;
if(remain_random_value <= ctx.rect_split_infos[base_index][0].self_prob)
{
return ctx.rect_split_infos[base_index][0].self_index;
}
else
{
return ctx.rect_split_infos[base_index][1].self_index;
}
}
上面介绍的方法也叫做Alias method,其更多的细节介绍可以参考https://www.keithschwarz.com/darts-dice-coins/。我自己也在Github上开源了一个简单的实现在https://github.com/huangfeidian/random_util/blob/main/include/choose_by_weight.h上,读者可以用这个基础代码作为参考实现。使用alias table算法就可以实现以常数时间来执行加权随机选择,所需的预处理时间也只是输入的线性时间。对于常见的十连抽一百连抽这种同一组配置会触发很多次随机选择的情况,这个算法是一个非常大的优化。
其实按照上面的代码流程构造出来的rect_split_infos可以保证rect_split_infos[i][0].self_index = i,可以利用这个性质来节省一点内存,不过这个性质对于算法的时间复杂度并没有任何改进,所以这里我就不去证明了,读者可以自己去证明这个性质。